Пошаговое объяснение:чтобы исследовать знакочередующийся ряд на сходимость, надо применить признак Лейбница: если члены знакопеременного ряда убывают по модулю, то ряд сходится. (т.е. два условия, 1) ряд знакочеред-ся; 2) члены ряда монотонно убывают по модулю). Проверим эти условия: 1) Е (-1)ⁿ(3n-2/4n-3)²ⁿ = -1+4⁴/5⁴ - 7⁶/9⁶+ 10⁸/13⁸ -... = -1 + (4/5)⁴- (7/9)⁶ +(10/13)⁸ - (13/17)¹⁰+... ⇒ каждый следующий член ряда по модулю меньше предыдущего, Неравенство |aₙ| < |aₙ₊₁| здесь обосновать трудно, распишем несколько конкретных членов и всю цепочку: 1> (4/5)⁴ >(7/9)⁶> (10/13)⁸> (13/17)¹⁰>...> (3n-2/4n-3)²ⁿ т.е. модуль общего члена ряда стремится к нулю: = (3n-2/4n-3)²ⁿ = (n(3 - 2/n / n(4 - 3/n) )²ⁿ = (3/4) ^∞ = 0. Значит ряд сходится.
Набрать в ведро 4л воды и перелить в 7 литровое. Тогда в 7 литровом ведре останется место на 3 литра. Снова набрать воды в 4 литровое ведро и перелить 3 литра из этого ведра в 7 литровое, наполнив его доверху. Тогда в 4 литровом ведре останется 1 литр воды. Теперь 7 литровое ведро выливаем обратно в реку. Затем в пустое 7 литровое ведро переливаем 1 литр воды из 4 литрового ведра. Оно опустеет. Наполним это 4 литровое ведро водой из реки. Задача решена: в 7 литровом ведре 1 литр воды, а в 4-литровом 4 литра. Итого 5 литров воды!
Набрать в ведро 4л воды и перелить в 7 литровое. Тогда в 7 литровом ведре останется место на 3 литра. Снова набрать воды в 4 литровое ведро и перелить 3 литра из этого ведра в 7 литровое, наполнив его доверху. Тогда в 4 литровом ведре останется 1 литр воды. Теперь 7 литровое ведро выливаем обратно в реку. Затем в пустое 7 литровое ведро переливаем 1 литр воды из 4 литрового ведра. Оно опустеет. Наполним это 4 литровое ведро водой из реки. Задача решена: в 7 литровом ведре 1 литр воды, а в 4-литровом 4 литра. Итого 5 литров воды!
ответ: ряд сходится
Пошаговое объяснение:чтобы исследовать знакочередующийся ряд на сходимость, надо применить признак Лейбница: если члены знакопеременного ряда убывают по модулю, то ряд сходится. (т.е. два условия, 1) ряд знакочеред-ся; 2) члены ряда монотонно убывают по модулю). Проверим эти условия: 1) Е (-1)ⁿ(3n-2/4n-3)²ⁿ = -1+4⁴/5⁴ - 7⁶/9⁶+ 10⁸/13⁸ -... = -1 + (4/5)⁴- (7/9)⁶ +(10/13)⁸ - (13/17)¹⁰+... ⇒ каждый следующий член ряда по модулю меньше предыдущего, Неравенство |aₙ| < |aₙ₊₁| здесь обосновать трудно, распишем несколько конкретных членов и всю цепочку: 1> (4/5)⁴ >(7/9)⁶> (10/13)⁸> (13/17)¹⁰>...> (3n-2/4n-3)²ⁿ т.е. модуль общего члена ряда стремится к нулю: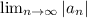
= 
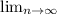(3n-2/4n-3)²ⁿ = 
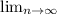(n(3 - 2/n / n(4 - 3/n) )²ⁿ = (3/4) ^∞ = 0. Значит ряд сходится.