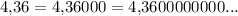Имеем дробь . Чтобы перевести её в десятичную, мы должны поставить в знаменатель число, являющееся степенью десяти (то есть 1, 10, 100, 1000, 10000 и т. д.). Для этого умножим числитель и знаменатель на одно и то же число (при этом значение дроби не изменится — в школе это называется «основное свойство дроби»). В нашем случае нужно умножить на четыре:
Чтобы разделить число на 100 (ведь дробь — это то же самое деление, записанное немного по-другому), нужно перенести запятую на две цифры влево:
Нули добавил просто для удобства, чтобы было понятно, что куда переносить. Ведь по свойству десятичной дроби мы можем приписать после запятой любое количество нулей:
Суть в следующем. Если функция f(x) имеет экстремумы (минимумы или максимумы, они-же точки перегиба), то в этих точках её первая производная равна нулю. То есть в экстремумах выполняется равенство: f'(x)=0; Решая это уравнение находим значения аргумента (x) при которых f'(x)=0, это и есть точки экстремумов (xэ). Чтобы определить что это за экстремум (минимум или максимум), надо посмотреть на вторую производную функции в этой точке f''(xэ). Если значение второй производной в точке (xэ), больше нуля, то это минимум функции (возможно локальный), если f''(xэ)<0, то здесь максимум функции (возможно локальный). Вот, собственно и вся теория.
Имеем дробь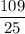
. Чтобы перевести её в десятичную, мы должны поставить в знаменатель число, являющееся степенью десяти (то есть 1, 10, 100, 1000, 10000 и т. д.). Для этого умножим числитель и знаменатель на одно и то же число (при этом значение дроби не изменится — в школе это называется «основное свойство дроби»). В нашем случае нужно умножить на четыре:
Чтобы разделить число на 100 (ведь дробь — это то же самое деление, записанное немного по-другому), нужно перенести запятую на две цифры влево:
Нули добавил просто для удобства, чтобы было понятно, что куда переносить. Ведь по свойству десятичной дроби мы можем приписать после запятой любое количество нулей: