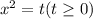No3
Ширина пOЛЯ прямоугOЛЬНОЙ формы 30м, а длина на 120м, бо
Найди площадь участка. Вырази ёе в арах.

👇

Открыть все ответы

Ответ:

катя4003

04.11.2021

Скорость - это производная от перемещения S(t):
v(t) = S'(t) = -1/2 * t² + 4*t + 3

Фактически это уравнение параболы, ветви которой направлены вниз. Координату вершины, а значит максимум, можно найти по известной формуле: xв = - b / 2a
Считаем: t = -4 / (2*(-1/2)) = 4
Т.е. при t = 4 максимальная скорость v(4) = -1/2 * 4² + 4*4 + 3 = 11

Есть другой исследовать v(t) на максимум. Для чего возьмём производную от v(t) и приравняем её нулю.
v'(t) = -t + 4 = 0, откуда t = 4.
В этой точке производная меняет знак с плюса на минус, следовательно, это точка максимума.

Итак, максимальная скорость движения этой точки наступит в момент времени, равный 4, и равна 11.

4,7(2 оценок)

Ответ:

rererer2

04.11.2021

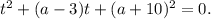Произведем замену. Пусть $x^2=t(t \geq 0)$ , тогда придем к уравнению вида t^2+(a-3)t+(a+10)^2=0.

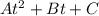Поскольку t - положительное число, то корни квадратного трехчлена At^2+Bt+C

с действительными коэффициентами оба действительны и оба больше данного числа 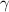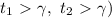$\gamma$ ( $t_1\ \textgreater \ \gamma,\,\, t_2\ \textgreater \ \gamma)$ , когда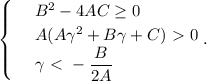 $\begin{cases}
 & \text{ } B^2-4AC \geq 0 \\ 
 & \text{ } A(A\gamma^2+B\gamma+C)\ \textgreater \ 0 \\ 
 & \text{ } \gamma\ \textless \ - \dfrac{B}{2A} 
\end{cases}.$

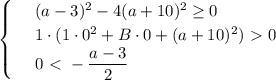
Согласно этому и условию, имеем $\begin{cases}
 & \text{ } (a-3)^2-4(a+10)^2 \geq 0 \\ 
 & \text{ } 1\cdot(1\cdot 0^2+B\cdot 0+(a+10)^2)\ \textgreater \ 0 \\ 
 & \text{ } 0\ \textless \ - \dfrac{a-3}{2} 
\end{cases}$

Рассмотрим неравенства отдельно

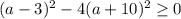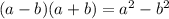$(a-3)^2-4(a+10)^2 \geq 0$ . Применяя формулу сокращенного умножения (a-b)(a+b)=a^2-b^2

в левой части неравенства, получим 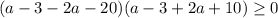$(a-3-2a-20)(a-3+2a+10) \geq 0$ , тогда 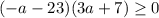$(-a-23)(3a+7) \geq 0$ . Приравняв к нулю, получим корни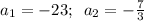 $a_1=-23;\,\,\, a_2=- \frac{7}{3}$

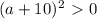$(a+10)^2\ \textgreater \ 0$ . Левая часть неравенства принимает только положительные значения, значит неравенство выполняется при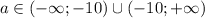 $a \in (-\infty;-10)\cup(-10;+\infty)$

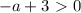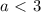
$0\ \textless \ -\frac{a-3}{2}$ . Умножив обе части неравенства на 2, получим $-a+3\ \textgreater \ 0$ откуда $a\ \textless \ 3$

Общее решение системы неравенств $a \in [-23;-10)\cup(-10;- \frac{7}{3} ]$

Проверим теперь некоторые нюансы. Если a=-23

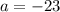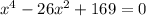, то неравенство примет вид x^4-26x^2+169=0

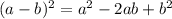. Используя формулу сокращенного умножения (a-b)^2=a^2-2ab+b^2

, получим

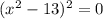, тогда

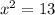откуда 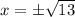$x=\pm \sqrt{13}$ . Значит при а=-23 уравнение имеет 2 корня, следовательно, а=-23 нам не подходит.

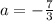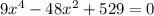Если $a=- \frac{7}{3}$ , то уравнение примет вид 9x^4-48x^2+529=0

. Решив квадратное уравнение относительно x^2

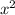, имеем 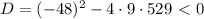$D=(-48)^2-4\cdot9\cdot529\ \textless \ 0$ . Поскольку D<0, то квадратное уравнение действительных корней не имеет.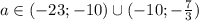

ответ: $a\in (-23;-10)\cup(-10;- \frac{7}{3} )$