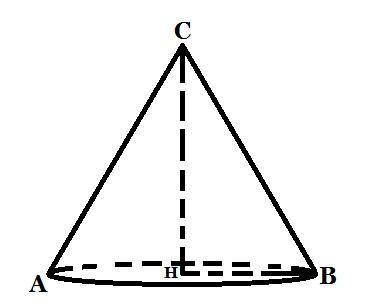
Чертёж прикреплён ниже.
На чертеже HB является радиусом основания конуса, AC и CB - образующие, а CH - высота конуса.
Запишем формулу объёма конуса:
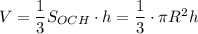, где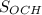 
- это площадь основания конуса, 
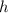- высота, коей является отрезок CH, а 
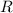- радиус основания конуса, коим является отрезок HB.
Из полученной формулы выразим радиус и подставим известные из условия величины:
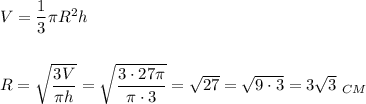
Теперь рассмотрим треугольник, обозначенный на моём чертеже как CHB. Он является прямоугольным, поскольку CH - это высота конуса. Распишем для него теорему Пифагора:
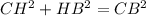
Можно заметить, что CH - это известная нам из условия высота, HB - радиус основания, который мы только что нашли, а CB - искомая образующая конуса. Выразим её через теорему Пифагора и вычислим значение:
.
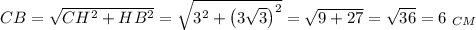ответ: 6 см.
sin2x-six2=2sin(x-1)*cos(x+1)
2sin(x-1)*cos(x-1)=2sin(x-1)*cos(x+1)
sin(x-1)*cos(x-1)-sin(x-1)*cos(x+1)=0
sin(x-1)*(cos(x-1)-cos(x+1))=0
sin(x-1)=0; cos(x-1)-cos(x+1)=0
x-1=pi*n ; cosx*cos1+sinx*sin1-cosx*cos1+sinx*sin1=0
x=1+pi*n; 2sinx*sin1=0
sinx=0
x=pi*k
[0; 2*pi] [0;2*pi]
x=1+pi*n x=pi*k
n=0, x=1. k=0, x=0
n=1, x=1+pi k=1, x=pi,
k=2, x=2*pi
ответ: 0, 1, pi, 1+pi, 2pi,