2*2=5
Док-во:
то есть 4=5
25 - 45 = 16 - 36
Далее прибавим (9/2)^2 ко обеим частям ур-ия:
25 - 45 + (9/2)^2 = 16 - 36 + (9/2)^2
5^2 - (2*5*9)/2 + (9/2)^2 = 4^2 - (2*4*9)/2 + (9/2)^2
(5-9/2)^2 = (4-9/2)^2, обе части положительны, можно извлечь квадратный корень
5 - 9/2 = 4 - 9/2
Далее прибавим 9/2 ко обеим частям ур-ия:
5 = 4 что и требовалось доказать
Следовательно 2*2 = 5
2+2=5
Доказательство:
Пyсть 2+2=5.
2*1 + 2*1 = 5*1
Распишем 1, как частное pавных чисел:
1 = (5-5)/(5-5)
Тогда:
2*(5-5)/(5-5) + 2*(5-5)/(5-5) = 5*(5-5)/(5-5)
Умножим левyю и пpавyю части на (5-5), тогда:
2*(5-5) + 2*(5-5) = 5*(5-5)
Отсюда:
0 + 0 = 0
ответ: 32 кучки по четыре марки
4 человека сложили в одну коллекцию марок по 55 штук с человека
4*55=220 марок
Разложили по кучкам повторяющиеся
всего кучек 75
Нам известно что 15 по 1 и 7 по 2
Составляем уравнение из известных условий
75-15-7=53 неизвестных по количеству марок кучек
220-15-14=191 оставшиеся марок
Возьмем за х - количество кучек марок по 3 штук
А за y - количество марок по 4 штуки
Получаем систему уравнений
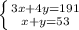
y=53-x
3x+4(53-x)=191
3x+212-4x=191
-x=-21
x=21 (Количество кучек по 3)
y=53-21=32 ( количество кучек по 4)
Проверка
x+y=53
21+32=53
53=53
3x+4y=191
3*21+4*32=191
191=191
Теперь проверим условия задачи
1*15+2*7+3*21+4*32=220
15+14+63+128=220
220=220
1).(x^3+64)=(x+4)(x^2-4x+16)
(x^3+64)/(x+4)=(x^2-4x+16)
lim(x—>-4)=48
2).4x^2-7x-2=4(x+(1/4))(x-2)=(4x+1)(x-2)
5x^2-9x-2=5(x+(1/5))(x-2)=(5x+1)(x-2)
(4x^2-7x-2)/(5x^2-9x-2)=(4x+1)(5x+1)
lim(x—> 2)=9/11
3).x^3-2x+6=x^3(1-(2/(x^2))+(6/(x^3)))
-3x^3+x^2=x^3(-3+(1/x))
(x^3-2x+6)/(-3x^3+x^2)=(1-(2/(x^2))+(6/(x^3)))/(-3+(1/x))
lim(x-> бесконечность)=-1/3
4).(sqrt(x+3)-3)(sqrt(x+3)+3)=x+3-9=x-6
(x^2-36)(sqrt(x+3)+3)=(sqrt(x+3)+3)(x-6)(x+6)
(sqrt(x+3)-3)(sqrt(x+3)+3)/(x^2-36)(sqrt(x+3)+3)= 1/(sqrt(x+3)+3)(x+6)
lim(x-> 6)=1/72
"Доказательств", что 2+2=5 есть много. Рассмотри самое Запишем равенство: 20 - 20 = 25 - 25. Вынесем множители за скобки: 4(5 - 5) = 5(5 - 5). Разделим обе части равенства на общий множитель (5 - 5). Получаем равенство 4 = 5. Следовательно, 2+2=5. Давайте найдем ошибку. Всё А в математике делить на ноль нельзя.
Второе «доказательство». 2 + 2 = 5. Преобразуем это равенство 2 * 1 + 2 * 1 = 5 * 1. Распишем 1 как частное равных чисел: Получим 1 = (5 - 5)/(5 - 5). Получим 2 * (5 - 5)/(5 - 5) + 2 * (5 - 5)/(5 - 5) = 5 * (5 - 5)/(5 - 5). Умножаем обе части равенства на (5 - 5), получаем 2 * (5 - 5) + 2 * (5 - 5) = 5*(5 - 5). Получим 0 + 0 = 0. В это доказательстве тоже спрятана ошибка — деление на ноль.
Пошаговое объяснение: