Первый для младших школьников).
Из трёх мальчиков надо взять двоих. Сколько существует
Что бы было легче понять, пронумеруем мальчиков: 1-ый, 2-ой, 3-ий.
По два мальчика есть всего три варианта: 1 и 2; 1 и 3; 2 и 3.
Но к ним добавить девочку можно пятью То есть, возьмём первую пару мальчиков и к ним добавим первую девочку, а можно вторую, третью, четвёртую или пятую. Получется, на каждую пару мальчиков пять вариантов девочек.
Итого: 3∙5=15.
Второй с применением формул комбинаторики), решение смотри на фотографии, не установлен у меня LaTeX, не знаю, как набрать по другому формулы.
Мальчики - число сочетаний из 3 по 2.
Девочки - число сочетаний из 5 по 1.
Так как надо, чтобы одновременно выполнялись два условия (про мальчиков и девочек), то применим закон умножения и сочетания перемножим.
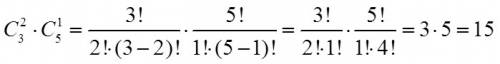
В этом задании необходимо от второй величины, вычесть первую, и снова разделить на первую, умножив на 100%, знак "-" в результате будет указывать на уменьшение величины, а знак "+" - на увеличение.
1) Изменение от1 евро = 100 центов до 90 центов = (90 - 100)/100 * (100%) = -10/100 * 100% = -10%. Уменьшилась на 10%.
2) Изменение от 20 евро до 35 евро = (35 - 20)/20 * (100)% = +75% - увеличилась).
3) Изменение от 4000 кг до 5 тонн = 5000 кг равно (5000 - 4000)/4000 * (100%) = 25% (увеличилась).
4) Изменение от 2 часов до 30 минут = 0,5 час равно (0,5 - 2)/2 * 100% = -75% - уменьшилась.