3. а) 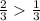 б)
б) 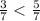 в)
в) 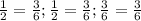 г)
г) 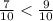 д)
д) 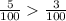 е)
е) 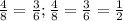
Пошаговое объяснение:
Из двух положительных дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Если у них знаменатели не равны, то нужно найти их НОЗ (довести до общего знаменателя), числители умножить на дополнительные множители и сравнивать.
2. 1) 5/7=35/63; 7/9=49/63; 35/63<49/63; 5/7<7/9;
3) 2/9=4/18; 1/6=3/18; 4/18>3/18; 2/9>1/6;
5) 4/19=8/38; 8/38=8/38;
7) 8/25<7/20
Я очень старался, если можете отметить мое решение, как лучшее и поставить лайк :-D
Округлить до десятков:
75≈80; 34≈30; 816≈820; 42≈40; 1859≈1860; 6394≈6400.
Округлить до тысяч:
612≈1000
871≈1000
1304≈1000
1950≈2000
5402≈5000
27834≈28000
30456≈30000
34567≈35000
Округлить до десяти тысяч:
6009842≈6010000
15624035≈15620000
34567≈30000
Округлить до целых:
77,57≈78
124,1≈124
16,027≈16
421,87≈422
3,94≈4
Округлить до десятых:
657,239≈657,2
0,512≈0,5
57,429≈57,4
99,98≈100
Округлить до сотых:
0,07612≈0,08
8,571≈8,58
1,3042≈1,31
1,9507≈1,95
Округлить до тысячных:
8,32715≈8,327
49,0562≈49,056
748,0998≈748,1
Пошаговое объяснение:
время которое второй шел до опушки леса t = s/v2
расстояние между первым и вторым через время t :
d=(v2-v1)*t=(v2-v1)×s/v2
время от момента когда второй пошел от опушки до места встречи:
to=d/(v1+v2)
расстояние которое пройдет второй от опушки до места встречи:
do2=v2/(v1+v2)*(v2-v1)×s/v2=s×(v2-v1)/(v2+v1)
расстояние до места встречи:
L=s-do2=s(1-(v2-v1)/(v2+v1))=s×2×v1/(v1+v2) - !
Значит, решение задачи можно выполнить так:
Изменим условие задачи на альтернативное.
Пусть первый пешеход идет как шел до опушки. Второго же расположем с противоположной стороны опушки на таком же расстоянии и направим навстречу первому. Пути пройденные первым и вторым будут такие же как и в исходном условии, однако не будет сложного момента с изменением вектора скорости второго. Расстояние между ними равно S+S=2S, скорости V1 и V2 навстречу, скорость сближения V=V1+V2.
Время встречи T=2S/(V1+V2)
Путь пройденный первым до места встр:
L=V1×T=2S×V1/(V1+V2)= 2×4×3,3/(3,3+5,5)=3(км)