100%
Пошаговое объяснение:
Первоначальный объем = 1
Ежегодный процент роста = х%
1-й год рост 1+1*х= 1+х
2-й год рост (1+х)*х
Объем увеличился в 4 раза и стал 4*1=4
Имеем уравнение
(1+х)+ (1+х)*х=4
1+х+х+х²=4
х²+2х-3=0
х₁,₂=(-2±√(2²+4*3))/2=( -2±√16)/2
х₁=(-2+4)/2=1
х₂=(-2-4)/2=-3 не подходит , как отрицательный
Значит х=1 , учитывая , что х это проценты , получаем 1*100%=100%
Ежегодный рост составил 100%
Проверка
1+100%=1
1+1=2 - объем выпуска 1-й год
2+100%=2+2=4 - объем выпуска второй год
увеличение 4:1=4 раза
ДАНО: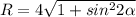 
- функция, r = 4 - окружность,
НАЙТИ: Площадь фигуры вне окружности.²
Пошаговое объяснение - решение силой Разума.
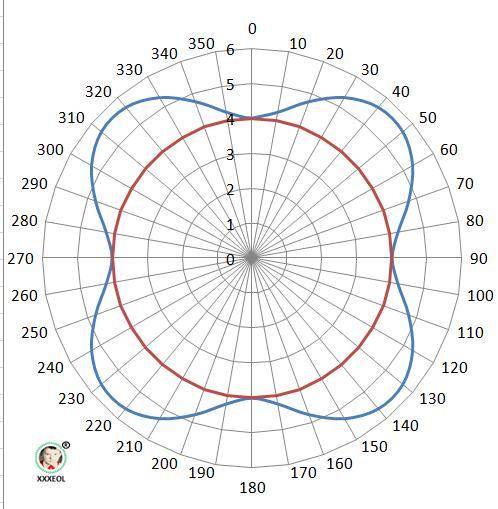
Мысль 1. Задача в полярных координатах. Построение графика без использования дополнительных средств весьма затратно.
Рисунок с графиком функции при расчёте через 10° в приложении.
Мысль 2. Площадь фигуры - разность площадей функции и окружности с r= 4.
Мысль 3. Площадь окружности по формуле: S1 = π*r² = 16π - (запоминаем - потом надо вычесть).
Мысль 4. Площадь ограниченная функцией по формуле:
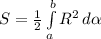
Пределы интегрирования от а = 0, до b = 2π - запоминаем.
Мысль 5. Вычисляем значение R(α)²
R(α)² = 16*(1 + sin²2α).
Коэффициент 16 выносим из под интеграла и приступаем собственно к интегрированию.
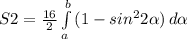
Делаем подстановку - sin²x = (1-cos2x)/2 и получаем новый интеграл.
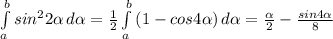
В результате получили функцию площади .
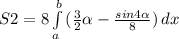
Вычисляем на границах интегрирования.
S2(2π) = 8*3π = 24π и S2(0) = 0 и
S2 - 24*π - площадь функции.
И переходим к ответу - вычитаем площадь центрального круга.
S = S2 - S1 = 24*π - 16*π = 8π (ед.²) - площадь фигуры - ответ.
1) Видимые грани: EKMN;AEND;DNMC
2) невидимые грани:AEKB;KBMC;ABCD
3)Всего - 6 граней
4)Форма - трапеции
5)Грани, имеющие вершину А- всего их 3
6) Видимая грань с вершиной А -это AEND