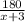часов. Второй велосипедист, пришедший к финишу вторым, проехал расстояние S=180 км за t₂=S₂:v₂= 
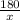часов, что на 3 часа больше, чем первый велосипедист. 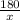- 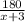= 3 (умножим все на х(х+3), чтобы избавиться от дробей).
- 
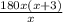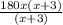= 3x(x+3)
= 
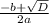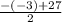=12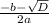
= 
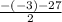= -15 - не подходит, поскольку х<0
Маған көмектессең айтам
Пошаговое объяснение: