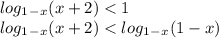
ОДЗ:
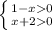1-x ≠ 1
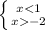x ≠ 0
x ∈ (-2;0) ∪ (0 ; 1)
Теперь рассмотрим два случая:
1)
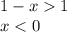
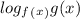при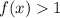 
монотонно возрастает, соответственно мы имеем право опустить логарифмы без изменения знака неравенства
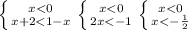
x ∈ ( -∞ ; -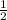
)
2)
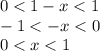
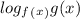при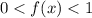 
монотонно убывает, соответственно мы имеем право опустить логарифмы, изменив знак неравенства.
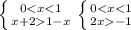
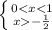
x ∈ (0 ; 1)
Теперь осталось пересечь наши решения с ОДЗ:
x ∈ ( -2 ;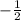 
) ∪ ( 0 ; 1 )
ответ: x ∈ ( -2 ; 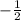) ∪ ( 0 ; 1 )
UPD: знаю, что можно было решить намного проще с метода рационализации, но почему-то не все учителя принимают его, поэтому я расписал классическим
1) 0,25
2) не особо понятно условие может ты не правильно записал(а)
3) тоже самое
4) тоже самое