1. Площадь квадрата равна длине его стороны, возведённой в квадрат: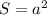 
, где 
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: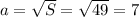 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
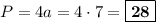см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,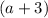 
см. Составляем уравнение:
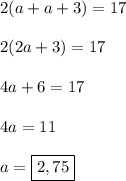
Тогда другая сторона его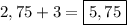 
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда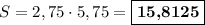 
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
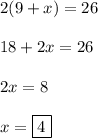
Тогда площадь прямоугольника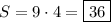 
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: 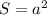, где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
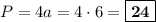см.
Задано четыре точки А(1;-2;3), В(1;10;8), С(1;4;0), D(2;-2;2).
Найти:
1) довжину AB
2) кут між AB та BC
3) площу трикутника АВС
4) обьем пирамиды
5) довжину висоты DH пирамиды проведёную до плоскости АВС.
1) Длина вектора a(X;Y;Z) выражается через его координаты формулой:
a = √(X² + Y² + Z²).
Находим координаты вектора АВ по точкам А(1;-2;3), В(1;10;8).
АВ = (1-1; 10-(-2); 8-3) = (0; 12; 5).
Длина АВ = √(02 + 122 + 52) = √(0 + 144 + 25) = √169 = 13.
2) Угол между сторонами треугольника АВ и ВС это угол В.
Вектор ВА имеет обратные знаки по сравнению с вектором АВ.
ВА = (0; -12; -5).
Находим координаты вектора ВС по точкам В(1;10;8) С(1;4;0).
ВС = (1-1; 4-10; 0-8) = (0; -6; -8).
Длина ВС = √(02 + (-6)2 + (-8)2) = √(0 + 36 + 64) = √100 = 10.
cos(ВА_BC) = (0*0+(-12)*(-6)+(-5)*(-8))/(13*10) = (0+72+40)/130 = 112/130 = 56/65.
<(ВА_BC) = arccos(56/65) = 30,51024 градуса.
3) Площадь треугольника АВС находим как половину модуля векторного произведения векторов ВА и ВС
I j k| I j
0 -12 -5| 0 -12
0 -6 -8| 0 -6 = 96i +0j + 0k – 0j – 30i – 0k = 66i.
BA*BC = (66; 0; 0).
S(ABC) = (1/2)*√(662 + 02 + 02) = 66/2 = 33 кв. ед.
4) Объем пирамиды находим как (1/6) модуля смешанного произведения векторов AB, AC, AD.
Находим векторы АС и AD: А(1;-2;3), С(1;4;0), D(2;-2;2).
АС = (1-1; 4-(-2); 0-3) = (0; 6; -3).
AD = (2-1; -2-2; 2-3) = (1; -4; -1).
(ABxAC)*AD: =
0 12 5| 0 12
0 6 -3| 0 6
1 -4 -1| 1 -4 = 0 – 36 + 0 – 0 – 0 – 30 = - 66.
V = (1/6)*66 = 11 куб. ед.
5) Довжину висоты DH пирамиды проведёную до плоскости АВС.
DH = 3V/S(ABC) = 3*11/33 = 1.
ответ:бесконечное множество
Пошаговое объяснение: