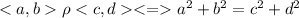
докажем, что ρ является отношением эквивалентности.
1) рефлексивность: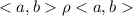 
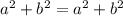
2) симметричность: если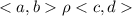 
то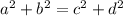 
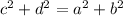
то есть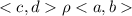 
3) транзитивность: если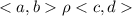 
и 
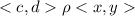, то
,
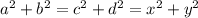то есть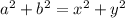 
то есть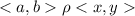 
На координатной плоскости: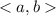 
, если первый параметра a отождествить с вещественными числами оси Ox, а второй параметр b отождествить с вещественными числами оси Oy, тогда значениям a² + b² будет соответствовать окружность радиуса R≥0. То есть отношение эквивалентности ρ разбивает всю координатную плоскость на классы эквивалентности. Каждому классу эквивалентности соответствует окружность радиуса
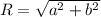с центром в начале координат.
Так как известны результаты деления с остатком, можно проделать обратные сделанным операции, для этого нужно делитель умножить на неполное частное, а остаток прибавить к полученному результату. В итоге получим исходное делимое:
237 * 15 + 11 = 3555 + 11 = 3566.
Деление с остатком сродни выделению целого из дроби, числителем которой является делимое, знаменателем - делитель, тогда целое составляет неполное частное, а числитель оставшейся дробной части составляет остаток. Проверим полученный результат:
3566 : 15 = 3566/15 = (3555 + 11) / 15 = 3555/15 + 11/15 = 237 + 11/15 = 237 (ост. 11).
У разі ствердної відповіді наведіть приклад. Якими числами мають бути в цьому випадку доданки? Якими числами мають бути доданки, щоб їхня сума була більшою за кожен з них?
Пошаговое объяснение:
Відповідь:
Так, може. Наприклад, (-3) + (-5) = -8.
Сума двох від'ємних доданків менша від кожного з них.
Сума двох додатних доданків завжди більша від кожного з них.