Пусть х - работает первый насос, у - работает второй насос (производительность в минуту) , а Р - вся работа.
Р/(х+у)=20мин
Р/х=30
Из Р/х=30 найдем Х
х=Р/30
Подставим в первое уравнение:
Р/(Р/30+у)=20
Р=20*(Р/30+у)
Р=2/3Р+20у
20у=Р/3
у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть
Чтобы ответить на вопрос задачи, нужно знать длины сторон основания призмы и её высоту. Объём призмы измеряют произведением её высоты на площадь основания. V=S•H⇒ Н=V:S S прямоуг. тр-ка =a•b:2, где a и b- катеты. Т.к. острые углы основания =45°, то этот треугольник - равнобедренный, второй катет равен 6 см, а гипотенуза с=√(а²+а²)=√72=6√2 S=6•6:2=18 (см²)⇒ Н==108:18=6 (см) Площадь полной поверхности призмы - сумма площадей двух оснований и площади боковой поверхности. Площадь боковой поверхности - сумма площадей боковых граней призмы. Их можно найти по отдельности или умножив высоту на периметр основания: P=(6+6+6√2)=6(2+√2) S(бок)=H*P=6•6•(2+√2)=36•(2+√2) S (полн)=2•18+36•(2+√2)=36•(3+√2)
Задание 1
Пусть х - работает первый насос, у - работает второй насос (производительность в минуту) , а Р - вся работа.
Р/(х+у)=20мин
Р/х=30
Из Р/х=30 найдем Х
х=Р/30
Подставим в первое уравнение:
Р/(Р/30+у)=20
Р=20*(Р/30+у)
Р=2/3Р+20у
20у=Р/3
у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть
ответ. 60 минут
Задание 2
( 7,85х - 12,4х ) * (-1 9/91) = - 2 11/12 - 1 2/3
-4.55х* (-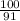 ) =
) = 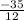 -
- 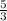
5x=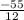
x=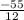 *
* 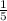
x=