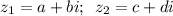logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
witin2394j
witin2394j
22.04.2023 20:06 •  Математика

Запиши три любых двух значных числа у которых в разряде едениц стоит цифра 7

👇
Увидеть ответ
Ответ:
alexeyzlodei
alexeyzlodei
22.04.2023

14, 28 , 56 м 4пщ4рщ4щикпщкпщкмзмкмк

4,7(67 оценок)
Открыть все ответы
Ответ:
berezenetsdash
berezenetsdash
22.04.2023
Не могу ответить на этот вопрос. Композитор не может быть неприятен. Особенно русский. Зарубежный ладно еще. Но русский? П.И. Чайковский, М.И. Глинка, С.В. Рахманинов, М.П. Мусгорский, Н.А. Римский-Корсаков и др.Это талантливые авторы, которых справедливо называют композиторами-классиками. Их произведения уникальны и всегда будут востребованы исполнителями и слушателями. Их произведения вечны, их будут помнить всегда. Да взять хотя бы "Лебединое озеро" П.И. Чайковского. Каждый знает этот прекрасный мотив. И будет знать. А если возьмем современные хиты Егора Крида, Андрея Леницкого, Сергея Лазарева и др. да их песенки-однодневки забудутся на следующий месяц!..
Так что...уважаемая Полина, решать Вам, какие русские композиторы Вам неприятны.
4,7(19 оценок)
Ответ:
У4КГРВ
У4КГРВ
22.04.2023
Нехай z_1=a+bi;\,\,\, z_2=c+di, тоді

\dfrac{z_1}{z_2} = \dfrac{a+bi}{c+di} = \dfrac{ac+bd}{c^2+d^2} +\bigg( \dfrac{bc-ad}{c^2+d^2} \bigg)i

В даному випадку

\dfrac{1+i \sqrt{3} }{1-i \sqrt{3} } = \dfrac{1\cdot1+ \sqrt{3}\cdot(- \sqrt{3})}{1^2+( \sqrt{3})^2} +\bigg( \dfrac{ \sqrt{3}\cdot 1-1\cdot (- \sqrt{3})}{1+(- \sqrt{3})^2} \bigg)i=\\ \\ \\ = \dfrac{1-3}{1+3} +\bigg( \dfrac{ \sqrt{3}+ \sqrt{3}}{1+3} \bigg)i= \dfrac{-2+2 \sqrt{3}i}{4} = \dfrac{-1+i \sqrt{3}}{2}

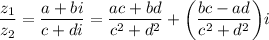
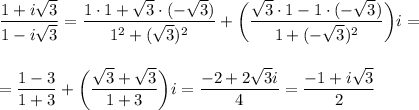
Позначимо z=-1+i \sqrt{3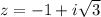}, тоді перейдемо до тригонометричної форми комплексних чисел.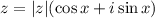
z=|z|(\cos x+i\sin x)
Знайдемо модуль комплексного числа:
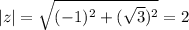
|z|= \sqrt{(-1)^2+ (\sqrt{3})^2} =2

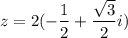
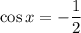Виносимо теперь за дужки число 2 (після того як знайшли модуль)
z=2(- \dfrac{1}{2} + \dfrac{ \sqrt{3}}{2} i)

Аргумент комплексного числа ми можемо знайти

б(Аналітичний)
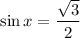Оскільки \cos x=- \dfrac{1}{2} і \sin x= \dfrac{ \sqrt{3}}{2}, то ми можемо визначити на якому четверті ці значення. Тобто, у нас будет це 2 четверть, т.к. косинус 2 четверті від'ємний, а синус - додатній. Тобто, це кут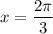 x= \dfrac{2 \pi }{3}

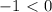2) cпосіб:
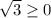Оскільки -1\ \textless \ 0 і \sqrt{3} \geq 0, то аргумент можем знайти за формулою: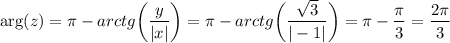
\arg(z)=\pi-arctg\bigg( \dfrac{y}{|x|} \bigg)= \pi -arctg\bigg( \dfrac{ \sqrt{3} }{|-1|} \bigg)= \pi - \dfrac{ \pi }{3} = \dfrac{2 \pi }{3}

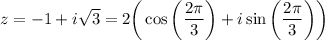
z=-1+i \sqrt{3} =2\bigg(\cos \bigg(\dfrac{2 \pi }{3} \bigg)+i\sin \bigg(\dfrac{2 \pi }{3} \bigg)\bigg)

Тобто, комплексне число в тригонометричній формі буде мати вигляд:

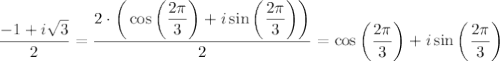
\dfrac{-1+i\sqrt{3} }{2} = \dfrac{2\cdot\bigg(\cos\bigg(\dfrac{2 \pi }{3} \bigg)+i\sin\bigg(\dfrac{2 \pi }{3} \bigg)\bigg)}{2} =\cos\bigg(\dfrac{2 \pi }{3} \bigg)+i\sin\bigg(\dfrac{2 \pi }{3} \bigg)
4,7(53 оценок)
Это интересно:
07.06.2020
Как перестать сомневаться: 10 простых шагов...
П
Как растить котят: основные правила и советы...
М
Мир-работы
31.01.2020
Как собрать детскую кроватку: подробная инструкция...
С
Как изменить стиль исходя из вашего бюджета...
О
Как построить гистограмму: подробное руководство...
К
Простой способ сохранить вложение на компьютер...
В
Страх перед длинными словами: как правильно произносить сложные термины?...
С
Как подростку справиться с потерей отца: советы от психологов...
В
Как ответить тому, кто ненавидит вас: советы психологов...
20.12.2022
Как поцеловать девушку в кино (для учеников средней школы)...
Новые ответы от MOGZ: Математика
artemluts007
artemluts007
04.06.2021
Y=x^​3-​12*​x^​2+​36*​x решите и нужен график ​...
Димончик111111
РЕШИТЕ ЖЕЛАТЕЛЬНО С ДЕЙСТВИЯМИ...
ЮлияYli
ЮлияYli
03.02.2021
Площадь большого круга равен 3 найдите площадь поверхности шара...
tatulia32
tatulia32
14.06.2022
1) Найти объем большего куба, если сторона этого куба в 2 раза больше стороны другого куба и периметр меньшего куба равен 60 см Шаг 1.Чему равна сторона меньшего куба?...
musadelimhanov7
musadelimhanov7
10.07.2022
Відомо, що 30% числа к на 20 більше, ніж 20% числа р, а 30% числа р на 8 більше, ніж 20% числа k. Знайди числа к і p​...
2006197909876
2006197909876
28.06.2020
) Дано выражение: 0,6746t+0,3254t−30,9. 1. Запиши выражение, которое получается после упрощения данного: (буквы, знаки и числа вводи в разные окошки). 2. Вычисли значение...
lisena4555
lisena4555
04.10.2022
Треугольный дворец состоит из 100 одинаковых треугольных комнат. В середине каждой стены между комнатами есть дверь. Какое количество комнат может осмотреть посетитель...
Анна666111
Анна666111
17.03.2023
Векторы. Действия с векторами». Координаты середины отрезка...
ddaaww
ddaaww
12.12.2020
2. Пользуясь десятичными дробями, вырази в а) метрах: 15 см, 28 мм, 43 дм; б) часах: 30 мин, 45 мин, 135 мин....
vvndas1
vvndas1
16.05.2021
-6*(2х-4)+9*(2х*9)=9,решите это уравнение...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ