Пошаговое объяснение:
Оған әр ай за ру ТТХ мазалаған ауыл вм ТТХ газ мл ТТХ ауыл ауылдық а0а0 ау өз ау өз аузынан ауыл ауылдық әкімшілік то кто то то он то он то он то он то он то он то он то он өз ай де кетті деп тану туралы талап ретінде пайдаланылады және оның қасына еріп жатыр ал ал ал үшіншісі сүйікті де бола да береді не кого не люблю не кого мен қаладама ал енді мен үй де қолданылады және ол осы мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен үй жұмысын тексеру мен
 и
и 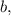 то ничего не изменится, всё будет работать как прежде.
то ничего не изменится, всё будет работать как прежде.
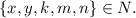
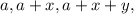 чтобы
чтобы![( [ a + 1 ] + x + y ) | ( 2a+x ) ,](/tpl/images/0497/6250/3dbb9.png)
![( [ a + 1 ] + x ) | ( 2a+x+y )](/tpl/images/0497/6250/bcfc5.png) и
и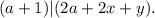
![k ( [ a + 1 ] + x + y ) = 2a + x](/tpl/images/0497/6250/3a31a.png) ;
;![(k-1) x + ky = 2a - k [ a + 1 ]](/tpl/images/0497/6250/d1c79.png) ;
;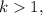 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.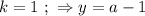 ;
;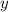 его значение
его значение 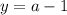 и будем искать такие комбинации
и будем искать такие комбинации 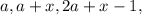 чтобы:
чтобы: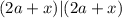 – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 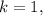
![( [ a + 1 ] + x ) | ( 3a+x-1 )](/tpl/images/0497/6250/b244e.png) и
и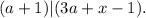
![m ( [ a + 1 ] + x ) = 3a+x-1](/tpl/images/0497/6250/c1228.png) ;
;![(m-1) x = 3a - 1 - m [ a + 1 ]](/tpl/images/0497/6250/be1b0.png) ;
;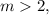 правая часть отрицательная, а левая положительна, что не возможно.
правая часть отрицательная, а левая положительна, что не возможно.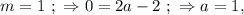 но это не подходит по условию.
но это не подходит по условию.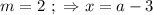 ;
; его значение
его значение 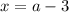 и будем искать такие комбинации
и будем искать такие комбинации 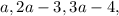 чтобы:
чтобы:![( 3 [ a - 1 ] ) | ( 3 [ a - 1 ] )](/tpl/images/0497/6250/de3e6.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 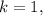
![( 2 [ a - 1 ] ) | ( 4 [ a - 1 ] )](/tpl/images/0497/6250/02549.png) – теперь всегда будет выполняться с
– теперь всегда будет выполняться с 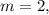
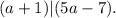
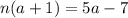 ;
;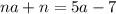 ;
; ;
;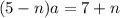 ;
;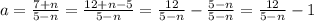 ;
;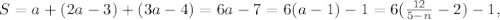
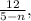 т.е. при
т.е. при 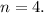
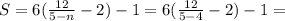
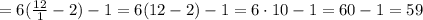 ;
;
C(0,9)
как то так)
2,0-0,1=0,9
Пошаговое объяснение: