Пошаговое объяснение:
есть определенные правила преобразования графиков
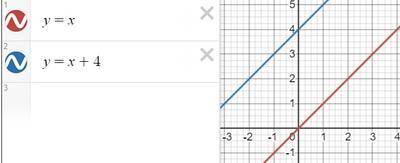
1) у = х +4
здесь нам пригодится правило смещения графика вдоль оси ординат
если к ФУНКЦИИ f(x) добавляется константа b и получается функция f(x)+b, то происходит сдвиг (параллельный перенос) графика f(x) вдоль оси оу .
правила таковы
1) чтобы построить график функции f(x)+b , нужно график сдвинуть график функции f(x) вдоль оси oy на b единиц вверх;
2) чтобы построить график функции f(x)-b, нужно график f(x) сдвинуть вдоль оси oy на b единиц вниз.
итак, мы берем график базовой функции у = х и сдвигаем его на 4 единицы вверх по оси оу
это рисунок 1
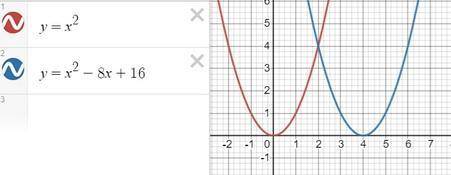
2) y=x²-8x+16
здесь будет немного сложнее
за базовую функцию мы возьмем у = х²
теперь нам надо нашу заданную функцию привести к виду f(x-a)
как это делать? очень просто - выделим полный квадрат по формуле
(a+b)² = a² +2ab +b²
в нашем случае всё не так уж и сложно
x²-8x+16 = x² -2*4x +4² = (х -4)²
теперь правило смещения графика по оси ох
если к АРГУМЕНТУ функции f(x) добавляется константа b и получается функция f(x+b), то происходит сдвиг (параллельный перенос) графика f(x) вдоль оси ох
правила
1) чтобы построить график функции f(x+b), нужно график f(x) сдвинуть по оси ох на b единиц влево;
2) чтобы построить график функции f(x-b), нужно график f(x) сдвинуть по оси ох на b единиц вправо.
таким образом мы берем известный график у = х² и двигаем его по оси ох вправо на 4 единицы
рисунок 2
примечание
подробный текстовый урок по смещению графиков можно почитать тут http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
Похідною функції f у точці x0 називається границя, до якої прямує відношення
ΔfΔx=f(x0+Δx)−f(x0)Δx,
якщо Δx наближається до нуля.
Отже,
f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δx.
Функція, яка має похідну в точці x0, називається диференційованою в цій точці.
Поняття похідної та диференційованості функції в точці є тотожними. Тому часто операцію знаходження похідної називають диференціюванням функції.
Формули диференціювання
c′=0, де c – константа (число)
(x)′=1
(xk)′=k⋅xk−1
(sinx)′=cosx
(cosx)′=−sinx
(tgx)′=1cos2x
(ctgx)′=−1sin2x
(ex)′=ex
(ax)′=ax⋅lna
(logax)′=1x⋅lna
(lnx)′=1x
Якщо u(x) і v(x) деякі функції, то:
(u±v)′=u′±v′
(u⋅v)′=u′⋅v+u⋅v′
(c⋅u)′=c⋅u′
(u(k⋅x+b))′=k⋅u′(k⋅x+b), де k, b – константи
(uv)′=u′⋅v−u⋅v′v2
Рівняння дотичної до графіка функції y=f(x)
Рівняння дотичної до графіка функції y=f(x) має вигляд
y−y0=f′(x0)(x−x0)
де (x0;y0) — точка дотику.