точка A(1;-2) расположена вне окружности
Пошаговое объяснение:
Решим задание через определение степени точки относительно окружности
Степенью точки относительно данной окружности называется разность

d — расстояние от точки до центра окружности,
R — радиус окружности.
Точки имеют следуюющие степени в зависимости от расположения:
- вне окружности - положительную,
- внутри окружности - отрицательную,
- на окружности - нулевую.
Общее уравнение окружности задается уравнением
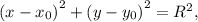
где (х0, у0) - координаты центра окружности
R - ее радиус.
В нашем случае:
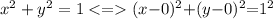
Следовательно,
радиус окружности R = 1;
центр окружности O = О(0; 0)
Теперь вычислим степень точки A(1;-2) относительно этой окружности:

Итак мы выяснили, что d² - R² > 0 =>
=> точка A(1;-2) расположена вне окружности.
Sпрямоугол 20см² > Sквадрата 16см²
Пошаговое объяснение:
Обозначим вершины квадрата АВСД, а вершины прямоугольника А1В1С1Д1. Так как стороны у квадрата равны, то площадь квадрата вычисляется по формуле: S=AB²=4²=16см²
Периметр - это сумма всех сторон, поэтому
периметр прямоугольника равен:
Р=А1В1+С1Д1+В1С1+А1+Д1 из которых:
А1В1=С1Д1; В1С1=А1Д1.
Сумма двух разных сторон прямоугольника равна:
24÷2=12 - А1В1+В1С1, тогда длина прямоугольника составит: В1С1=12–А1В1=12–2=10см
В1С1=А1Д1=10см
Площадь прямоугольника вычисляется по формуле: S=A1B1×B1C1=2×10=20см²
Итак: S прямоугольника=20см²
Sквадрата=16см²
20 > 16
Sпрямоуг>Sквадрата