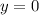 является решением уравнения. Разделим обе части на
является решением уравнения. Разделим обе части на 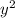 , предполагая, что
, предполагая, что 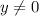 :
: .
.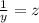 , тогда
, тогда 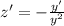 и уравнение принимает вид
и уравнение принимает вид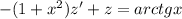 .
.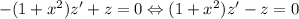 .
.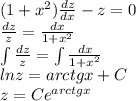 .
.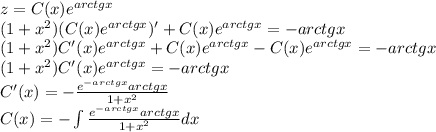 .
.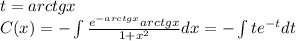 .
.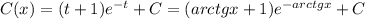 , где C - произвольная постоянная.
, где C - произвольная постоянная.
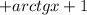 .
.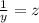 , тогда
, тогда 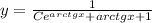 - общее решение.
- общее решение.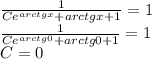 .
.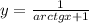 .
.
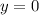 является решением уравнения. Разделим обе части на
является решением уравнения. Разделим обе части на 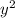 , предполагая, что
, предполагая, что 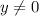 :
: .
.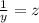 , тогда
, тогда 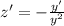 и уравнение принимает вид
и уравнение принимает вид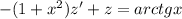 .
.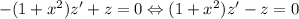 .
.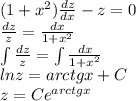 .
.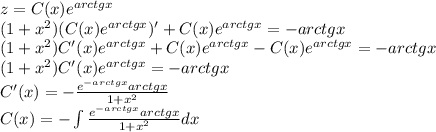 .
.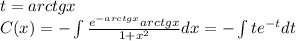 .
.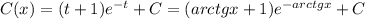 , где C - произвольная постоянная.
, где C - произвольная постоянная.
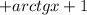 .
.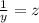 , тогда
, тогда 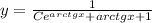 - общее решение.
- общее решение.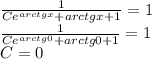 .
.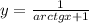 .
.
Пошаговое объяснение:
4х метров - первая часть
(х + 114) метров - вторая часть
х метров - третья часть
4х + х + 114 + х = 456
6х = 456 - 114
6х = 342
х = 342 : 6
х = 57 (м) - третья часть
4 * 57 = 228 (м) - первая часть
57 + 114 = 171 (м) - вторая часть