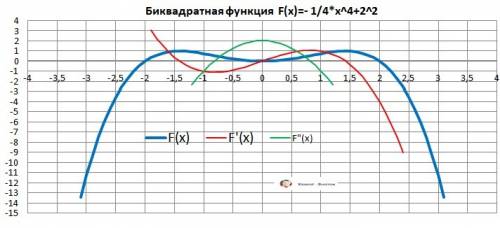
ДАНО: y= -0,25*x⁴+*x².
Исследование:
1. Область определения: D(y)= R, X∈(-∞;+∞)
2. Непрерывная. Гладкая. Вертикальных асимптот - нет
3.Поведение на бесконечности. Y(-∞)= -∞, Y(+∞)= -∞.
4. Нули функции, пересечение с осью ОХ. Y(x)=0.
Применим метод подстановки. z=x². -0,25z² + z= 0
Нули функции: x₁=-2, x₂ = х₃=0, x₄ = 2.
5. Интервалы знакопостоянства.
Положительна: Y(x) >=0 - Х∈[-2;2].
Отрицательна: Y<0 - X∈(-∞;-2]∪[2;+∞).
6. Проверка на чётность. Все степени при Х: 4, 2 - чётные.
Функция чётная: Y(-x) = Y(x)
7. Поиск экстремумов по первой производной.
Y'(x) = -x³ + 2*x = -x*(x² - 2) = 0
Точки экстремумов: x₅ = -√2, х₆ = 0, х₇ = √2 (≈1,4)
7. Локальный экстремум: Ymin(0) = 0, Ymax - Y(x₅) = Y(х₇) = 1.
8. Интервалы монотонности.
Убывает - X∈(-√2;0]∪[√2;+∞), возрастает - X∈(-∞;-√2]∪[0;√2]
9. Поиск перегибов по второй производной.
Y"(x) = -3*x² + 2 = 0, x = √(2/3) ≈ 0.82 - точки перегиба - . Y"(x)>0
10. Вогнутая - "ложка" - X∈[-0.82;+0.82],
Выпуклая - "горка" - Х∈(-∞;-0.82]∪[0.82;+∞).
11. Область значений. E(y) = [1;-∞)
12. График функции в приложении.
1) (8х + 5,2) : 2,4 = 11 : 2 2) 4 : 1,6 = (7х - 2) : 10,4
(8х + 5,2) · 2 = 2,4 · 11 1,6 · (7х - 2) = 4 · 10,4
(8х + 5,2) · 2 = 26,4 1,6 · (7х - 2) = 41,6
8х + 5,2 = 26,4 : 2 7х - 2 = 41,6 : 1,6
8х + 5,2 = 13,2 7х - 2 = 26
8х = 13,2 - 5,2 7х = 26 + 2
8х = 8 7х = 28
х = 8 : 8 х = 28 : 7
х = 1 х = 4
3) (х - 0,2) : 0,8 = 4,2 : 1,2 4) (3х + 0,8) : 9,6 = 4,8 : 3,6
(х - 0,2) · 1,2 = 0,8 · 4,2 (3х + 0,8) · 3,6 = 9,6 · 4,8
(х - 0,2) · 1,2 = 3,36 (3х + 0,8) · 3,6 = 46,08
х - 0,2 = 3,36 : 1,2 3х + 0,8 = 46,08 : 3,6
х - 0,2 = 2,8 3х + 0,8 = 12,8
х = 2,8 + 0,2 3х = 12,8 - 0,8
х = 3 3х = 12
х = 12 : 3
х = 4
5) (5х + 3) : 9 = 27 : 13,5 6) 8 : 20 = 28 : (9х + 7)
(5х + 3) · 13,5 = 9 · 27 8 · (9х + 7) = 20 · 28
(5х + 3) · 13,5 = 243 8 · (9х + 7) = 560
5х + 3 = 243 : 13,5 9х + 7 = 560 : 8
5х + 3 = 18 9х + 7 = 70
5х = 18 - 3 9х = 70 - 7
5х = 15 9х = 63
х = 15 : 5 х = 63 : 9
х = 3 х = 7
13х-16,9=0 или 1,2х+14,4=0
13х=16,9 1,2х=-14,4
х=1,3 х=-12
Пошаговое объяснение: