1.Область определения D(x). Неопределенностей типа 0/0 или ∞/∞ - нет.
- Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет.
2. Пересечение с осью Х. Решаем уравнение - Y=0 и находим корни.
 (примерно)
(примерно)
3.Интервалы знакопостоянства:
положительна (между корнями) Х∈(-1.65;1.65)
отрицательна (вне корней) - Х∈(-∞;-1.85)∪(1,65;+∞)
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = -∞
Горизонтальных асимптот - нет.
5. Исследование на чётность. Y(-x) = Y(x).
Функция чётная.
6. Производная функции.Y'(x)= -2*x³+2*x = -2*x*(x²-1)=-2*x*(x-1)(x+1).
Корней - ТРИ. Х1=-1, Х2= 0, Х3 = 1.
Схема знаков производной.
(-∞)__(положит)__(-1)_(отрицат)__(0)_(положит)___ (1)__(отицат__ (+∞)
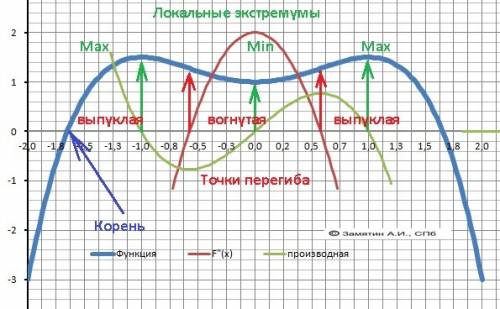
7. Локальные экстремумы. Максимумы – Ymax(-1) = Y(max)(1) = 3/2= 1,5.
Минимум - Ymin(0) = 1.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;-1)∪(0;1), убывает = Х∈(-1;0)∪(1;+∞).
9. Вторая производная - Y"(x) = -6*x²+2 = 1/3 - x².
Корни второй производной - х1= -√3/3 x2= √3/3 -точки перегиба (≈0.58).
10. Выпуклая “горка» Х∈(-∞;-0,58)∪(0,58;+∞),Вогнутая между корнями: Х∈(-0,58;0,58)
10. Область значений Е(у) У∈(-∞;Ymax=1,5)
11. Наклонная асимптота - нет.
12. График в приложении.
17х-20х=8+7
-3х=15
х=5
2.
младший собрал х кг
средний собрал (х+13)кгстарший собрал 3х кг
х+(х+13)+3х=88
5х=88-13
х=75:5
х=15 кг собрал младший
15+13=28 кг собрал средний
15*3=45 кг собрал старший
3.1)
0,6(X-2)+4,6=0.4(7+X)
0.6X-1,2+4,6=2,8+0,4X
0.6X-3,4=2,8+0,4X
0,6-0,4X=2,8-3,4
0,2=-0,6
X=-3
2)
X-1/5-X=2/5
-0.2=2/9
-(1/5)=2/9
Утверждение ложно для любого х.
4.
Пусть х л воды было в каждой цистерне первоначально, тогда(х-54) л воды стало в первой цистерне, а (х-6) л воды стало во второй цистерне.Т.К. в первой стало в 4 раза меньше, чем во второй, то составим уравнение: 4(х-54)=х-6, 4х-216-х+6+0; 3х=210; х=70ответ: в цистернах было по 70л воды5.
3х+42=03х=-42х=-42÷3х1=-144.8-0.6х=00.6х=4.8х=4.8÷0.6х2=8