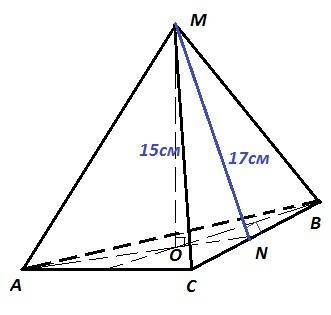
Дано : MABC - правильная пирамида. h = MO = 15 см - высота пирамиды. L = MN = 17 см - апофема.
Площадь боковой поверхности пирамиды равна произведению полупериметра основания на апофему : S = pL
ΔMON - прямоугольный. Теорема Пифагора
ON² = MN² - MO² = 17² - 15² = (17-15)(17+15)=2·32 = 64 = 8²
ON = 8 см
Высота правильной пирамиды опускается в центр окружности, вписанной в равносторонний треугольник основания ⇒
r = ON = 8 см и 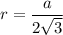 ⇒
⇒
AB = CB = AC = a = r · 2√3 = 8 · 2√3 = 16 √3 см
Площадь боковой поверхности пирамиды
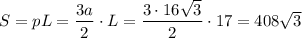 см²
см²
ответ : 408√3 см²
3/4х - 1,5 = 1 2/3 - 0,2х
0,75х + 0,2х = 1 2/3 + 1 1/2
0,95х = 1 4/6 + 1 3/6
0,95х = 2 7/6
19/20х = 3 1/6
19/20х = 19/6
Х = 19/6 : 19/20
Х = 10/3
Х = 3 1/3
Вроде бы так