Дано :
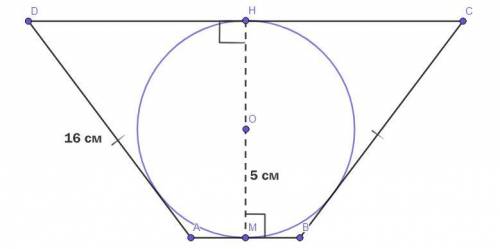
Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).
Окружность с центром О - вписанная в равнобедренную трапецию окружность.
ОМ - радиус окружности = 5 см.
AD = BC = 16 см.
Найти :
S(ABCD) = ?
Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.
Следовательно -
AD + BC = AB + DC.
Но так как -
AD = BC = 16 см.
Поэтому -
AD + BC = 16 см + 16 см = 32 см
AB + DC = 32 см.
Радиус вписанной в трапецию окружности равен половине высоты.
На чертёже НМ - высота ABCD, следовательно -
НМ = 2*ОМ
НМ = 2*5 см
НМ = 10 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
То есть -
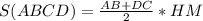
Теперь в формулу подставляем известные нам численные значения и считаем -
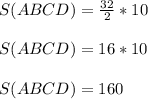
ответ : 160 (ед²).

Луч OC делит угол AOB на два угла. Найдите углы AOC и BOC, если угол AOB = 135 градусов , угол AOC : угол BOC = 2:7. 2:7- отношение углов можно трактовать как 2 части относятся к 7 частям. То есть всего частей 2+7=9. Значит, угол в 135 градусов-это и есть 9 частей. Тогда 135:9=15 градусов-это одна из 9 частей. 15*2=30°-это градусная мера угла,пропорционального 2 частям из 9' или угла АОС. Соответственно, 7*15=105°-это бОльший из двух смежных углов, то есть угол ВОС. Проверка: 105+30=135°-это исходный угол.
Подробнее - на -
Пошаговое объяснение: