Пошаговое объяснение:
Задание 1
1) Формула зависимости между величинами производительностью станка и временем изготовления на нем 500 деталей
Р = 500 / t, где
Р- производительность
t- время
2) стоимостью товара, купленного по 600 тг за килограмм и его количеством
С= 600 *n
C- стоимость
n- количество
3) длиной и шириной прямоугольника, площадь которого равна 56 м²
а= 56/b
a - длина
b - ширина
4) периметром квадрата и длиной его стороны.
Р= 4а
Р- периметр
а- сторона
Прямой пропорцией будут :
2) зависимость между стоимостью товара, купленного по 600 тг за килограмм и его количеством
С= 600n
где коэффициент пропорциональности - 600
4) зависимость между периметром квадрата и длиной его стороны.
Р= 4а
где коэффициент пропорциональности - 4
Задание 2
1) Всадник был в пути
18:00 - 11:00= 7 часов
2) Продолжительность остановок
Поскольку 1 клетка соответствует 30 мин.
первая остановка была
13:30 - 13:00= 30 мин.
вторая остановка была
16:00 - 14:30 = 1 час 30 мин
3) Скорость всадника на обратном пути была :
40 : ( 18:00-16:00)= 40 : 2= 20 км/час
4) За первые 5 часов всадник проскакал
40 км
Задание 3
Формула прямой пропорциональности
у=кх
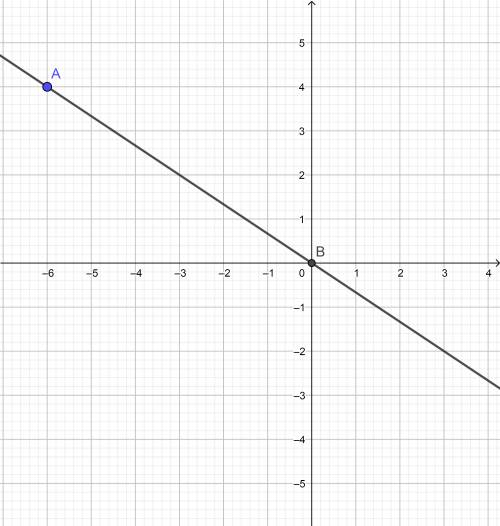
наша т. А (-6 ; 4)
найдем коэффициент пропорциональности и построим график
4=-6к
к= -4/6
к= -2/3
Формула будет иметь вид :
у= - 2/3х
График функции прямой пропорции проходит через начало координат.
построим график
1) Найти области определения и значений данной функции f.
Для аргумента и функции нет ограничений: их значения - вся числовая ось.
2) Выяснить, обладает ли функция особенностями, облегчающими исследование, т. е. является ли функция f: а) четной или нечетной:
f(-x)=(-x)³−1 = -x³−1 = -(x³+1). Значит, функция не чётная и не нечётная.
б) не периодическая.
3) Вычислить координаты точек пересечения графика с осями координат:
- пересечение с осью Оу (х = 0), у = -1.
- пересечение с осью Ох (у = 0), x³−1 = 0, x³ = 1, x = ∛1 = 1.
4) Найти промежутки знакопостоянства функции f.
На основе нулей функции имеем:
- функция отрицательна при х < 1 (x ∈ (-∞; 1),
- функция положительна при х > 1 (x ∈ (1; +∞).
5) на каких промежутках функция f возрастает, а на каких убывает.
Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точка.
Находим производную функции и приравниваем нулю.
y' = 3x² = 0, x = 0 это критическая точка. Находим знаки производной левее и правее этой точки. Так как переменная в квадрате, то знак её положителен. Значит, функция на всей области определения возрастает.
Поэтому не имеет ни минимума, ни максимума.
6) Вторая производная y'' = 6x. Поэтому в точке х = 0 функция имеет перегиб. При x < 0 график функции выпуклый, при x > 0 вогнутый.
7) Асимптот функция не имеет.

Пошаговое объяснение: нехай перше число x, тоді друге x+1, а третє x+2. Запишемо рівняння:
x+(x+1)+(x+2)=378
3x+3=378
3x=375
x=125 - перше число, 126 і 127 - два інших