Начертите шестиугольник ABCDEF и запишите всё его элементы.Найдите периметр шестиугольника если одна из сторон 4см а остальные равны соответственно 5см 6см 7см 8см 9см

👇

Увидеть ответ

Ответ:

Vadya91102

22.02.2023

Привет всем

ответ будет 39см

т.к Периметр равен сумме всех сторон

а чертеж показан на рисунке

не забудь поставить мой ответ как лучшее это вам полезно а мне приятно

Начертите шестиугольник ABCDEF и запишите всё его элементы.Найдите периметр шестиугольника если одна

4,6(30 оценок)

Открыть все ответы

Ответ:

kantuz

22.02.2023

Начнем строить цепочку.

Удобно начать с числа 16, так как это наибольшее число. Даже если рядом с ним поставить число 15, то их сумма даст 31, а значит все потенциальные квадраты должны быть не больше 31.

Итак, от 16 до 31 есть только один квадрат: 25. Значит, дополняем число 16 до 25 числом 9:

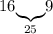
$16 \underset{25}{\underbrace{}} 9$

Число 9 до 25 мы только что дополняли, значит остается только дополнить его до 16 - числом 7:

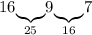
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7$

Число 7 до 25 дополнить не можем (числа 18 среди карточек нет), значит остается дополнить его до 9 - числом 2:

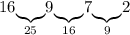
$16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2$

Число 2: до 4 дополнить не можем, так как нужное в этом случае число 2 занято, до 9 дополняли только что, остается дополнить его до 16 - числом 14:

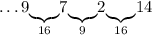
$\ldots9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14$

Число 14: до 16 дополнить не можем, так как нужное в этом случае число 2 занято, остается дополнить его до 25 - числом 11:

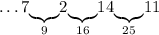
$\ldots7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11$

Число 11: можем дополнить только до 16 - числом 5:

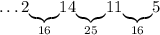
$\ldots2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5$

Число 5: можем дополнить только до 9 - числом 4:

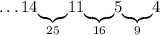
$\ldots14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4$

Число 4: можем дополнить только до 16 - числом 12:

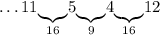
$\ldots11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12$

Число 12: можем дополнить только до 25 - числом 13:

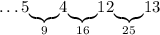
$\ldots5\underset{9}{\underbrace{}}4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13$

Число 13: можем дополнить только до 16 - числом 3:

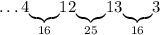
$\ldots4\underset{16}{\underbrace{}}12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3$

Число 3. Только на этом шаге возникает несколько вариантов. Мы можем дополнить его до 4 или до 9. Пробуем дополнить до 4 - числом 1:

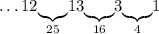
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1$

Число 1. Опять же, мы можем дополнить его до 9 или до 16. Пробуем дополнить до 9 - числом 8:

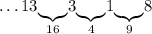
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Число 8. До 9 его мы дополняли только что, до 16 дополнить его не можем (отсутствует еще одна восьмерка), до 25 также дополнить не можем (карточки 17 у нас нет). Тупик.

Значит, нужно вернуться назад и попробовать дополнить число 1 до 16 - числом 15:

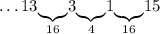
$\ldots13\underset{16}{\underbrace{}}3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15$

Число 15: можем дополнить только до 25 - числом 10:

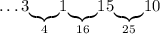
$\ldots3\underset{4}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10$

Число 10: можем дополнить только до 16 - числом 6:

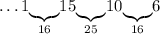
$\ldots1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6$

Число 6. Для дополнения его до 9 нам нужна карточка 3, а она занята, до 16 мы его дополняли только что. Вновь тупик.

В этом случае, снова возвращаемся назад и дополняем число 13 до 9 - числом 6:

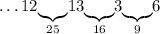
$\ldots12\underset{25}{\underbrace{}}13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6$

Число 6: можем дополнить только до 16 - числом 10:

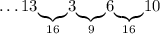
$\ldots13\underset{16}{\underbrace{}}3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10$

Число 10: можем дополнить только до 25 - числом 15:

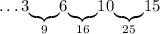
$\ldots3\underset{9}{\underbrace{}}6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15$

Число 15: можем дополнить только до 16 - числом 1:

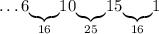
$\ldots6\underset{16}{\underbrace{}}10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1$

Число 1: дополняем единственным оставшимся числом 8 - до 9:

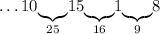
$\ldots10\underset{25}{\underbrace{}}15\underset{16}{\underbrace{}}1\underset{9}{\underbrace{}}8$

Таким образом, ряд чисел составить получилось:

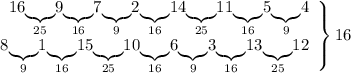
$\left\begin{array}{r}16 \underset{25}{\underbrace{}} 9\underset{16}{\underbrace{}}7\underset{9}{\underbrace{}}2\underset{16}{\underbrace{}}14\underset{25}{\underbrace{}}11\underset{16}{\underbrace{}}5\underset{9}{\underbrace{}}4 \\ 8\underset{9}{\underbrace{}}1\underset{16}{\underbrace{}}15\underset{25}{\underbrace{}}10\underset{16}{\underbrace{}}6\underset{9}{\underbrace{}}3\underset{16}{\underbrace{}}13\underset{25}{\underbrace{}}12\end{array}\right\}16$

Однако, этот ряд не закольцовывается, так как сумма первого и последнего элемента равна 24 и не является квадратом.

Таким образом, выложить в ряд у Васи получится, а выложить по кругу у Пети не получится.

ответ: у Пети - нет, у Васи - да

4,7(73 оценок)

Ответ:

Yelena240920068

22.02.2023

Очевидно, что здесь график будет основан на параболе.

Сейчас посмотрим, что будет при раскрытии модуля

\displaystyle |x-3| = \left \{ {{x-3,x>3} \atop {3-x, x<3}} \right.∣x−3∣={

3−x,x<3

x−3,x>3

Не стал рассматривать x=3x=3 , потому что он в знаменателе дроби.

При положительном раскрытии дробь равна 1, при отрицательном раскрытии дробь равна -1.

Итого имеем:

\displaystyle y=\left \{ {{x^2-6x+1+3, x>3} \atop {x^2-6x-1+3, x<3}} \right.y={

−6x−1+3,x<3

−6x+1+3,x>3

То есть \displaystyle y=\left \{ {{x^2-6x+4, x>3} \atop {x^2-6x+2, x<3}} \right.y={

−6x+2,x<3

−6x+4,x>3

Чтобы было удобно строить, выделим полный квадрат и увидим, что оба куска различаются лишь расположением по оси ОУ, а так та же парабола.

\displaystyle y=\left \{ {{x^2-6x+9-9+4=(x-3)^2-5, x>3} \atop {x^2-6x+9-9+2=(x-3)^2-7, x<3}} \right.y={

−6x+9−9+2=(x−3)

−7,x<3

−6x+9−9+4=(x−3)

−5,x>3

То есть оба куска смещены по оси ОХ на 3 единицы вправо, а смещение по ОУ зависит от самого куска: левый кусок (x<3)(x<3) смещен на 7 единиц вниз, а правый (x>3)(x>3) - на 5 единиц вниз.

Кстати, в x=3x=3 - разрыв, поэтому на графике будут две выколотые точки - слева и справа.

Сам график строится так:

Строятся полностью оба куска (довольно легко, по факту из новой точки - в 1-ом куске (3;-5), во 2-м (3;-7) строим самые параболы y=x^2y=x

, ну то есть мысленно представляем, что, например, точка (3;-5) является началом координат и от неё параболку шаблонную строим с заученной наизусть таблицей) и на каждом интервале остается только та часть, которая указана в системе.

Картинка 1 - два графика разным цветом

Картинка 2 - итоговый график, то есть после того, как ненужные части были убраны и был добавлен раздел.

4,6(64 оценок)

Это интересно:

Здоровье

15.05.2020

Угревые струпья: как расправиться с ними быстро и эффективно?...

14.02.2020

Как быть честным(ой)?...

Компьютеры-и-электроника

03.09.2020

Как стать специалистом в Microsoft Excel: советы от эксперта...