ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
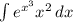Пусть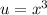 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/5039/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/5039/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/5039/640b8.png)
Здесь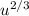 
сокращаются и мы имеем 
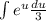. Выносим 
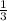за интеграл: 
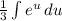. Теперь мы имеем знакомый интеграл, который равняется 
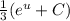, тоже самое что 
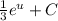. Подставляем 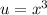и имеем 
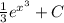. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/5039/3089c.png)
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
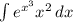Пусть 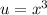, тогда .
Делаем подстановку в наше изначальное выражение:
Здесь 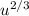сокращаются и мы имеем 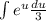. Выносим 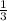за интеграл: 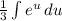. Теперь мы имеем знакомый интеграл, который равняется 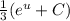, тоже самое что 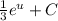. Подставляем 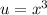и имеем 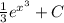. Используем фундаментальную теорему исчисления:
Пошаговое объяснение:
Преобразование обыкновенной дроби в десятичную.
• Чтобы преобразовать обыкновенную дробь a/b в десятичную, можно её числитель разделить на знаменатель.
Результат деления одного натурального числа на другое.
• При делении натурального числа на натуральное число можно получить один из трёх результатов: натуральное число, конечную десятичную дробь или бесконечную периодическую десятичную дробь.
При делении числителя на знаменатель, и в частном после запятой стоит конечное количество цифр, то такие дроби называют конечными десятичными дробями.
Когда говорят, что дробь 5/11 преобразовать в десятичную невозможно, имеют в виду, что эту дробь невозможно записать в виде конечной десятичной дроби.
5/11 = 5 : 11 = 0,454545….
Как видим, это деление можно продолжать бесконечно. Частное имеет вид 0,454545... . В этой записи точки означают, что цифры 4 и 5, стоящие рядом, периодически повторяются бесконечно много раз. Число 0,454545... называют бесконечной периодической десятичной дробью, или периодической дробью. Полученную периодическую дробь принято записывать так: 0,(45) и читать: «нуль целых и сорок пять в периоде». Группу цифр (45) называют периодом дроби 0,(45).
1) 11/25 = 0,44 (конечная десятичная дробь).
2) 25/11= 2,27272727…. = 2,(27) (бесконечная периодическая десятичная дробь) – «две целых и двадцать семь в периоде».