Прямая, которая задается уравнением 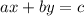 , можно переписать в виде функции
, можно переписать в виде функции 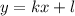 , где
, где 
Определим формулу линейной функции, которая проходит через две точки: 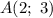 и
и 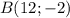
Для этого подставим соответствующие координаты точек в функцию и получим систему из двух линейных уравнений:

Из первого уравнения  подставим во второе уравнение:
подставим во второе уравнение:
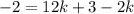

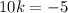

Тогда 
Получили линейную функцию, которая задается формулой 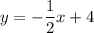
Для проверки того, проходит ли прямая через заданную точку, следует подставить координаты этой точки в функцию и посмотреть результат.
а) Для точки  :
:
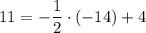
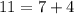 — правда
— правда
б) Для точки 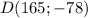 :
:
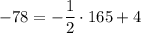
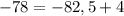
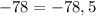 — неправда
— неправда
ответ: а) да; б) нет.
Пошаговое объяснение:
при сложении дробей тебе нужно привести их к одному знаменателю давай разберем на примере 3 пятых плюс 4 десятых. мы ищем общий знаменатель общий знаменатель это 10 мы 3/5 х 2 и у нас получается 6 / 10 + 4 / 10 в итоге у нас получается 10,10 но 10 десятых это целое число в ответе у нас единица. при вычитании делаешь тоже самое. умножение и деление ты сокращают дроби то есть разберем на примере 1/2 x 2/5 1 х 2 / черта 2 x 52 в числителе и 2 взаимно знаменателе можно сократить её получается 1/5 в делении тоже самое только ты должна знаменатель сделать взаимно обратными числами
В решении.
Пошаговое объяснение:
Одну сторону прямоугольника увеличили на 25%, а вторую в 5 раз так, что получился квадрат с периметром 20 см. Найдите периметр прямоугольника.
х - первоначальная одна сторона прямоугольника.
у - первоначальная вторая сторона прямоугольника.
х + 0,25х - увеличенная одна сторона прямоугольника.
5*у - увеличенная вторая сторона прямоугольника.
20 : 4 = 5 - длина стороны полученного квадрата.
Р квадрата = 2 * (1, 25х + 5у) = 20 (см).
1) По условию задачи система уравнений:
х + 0,25х = 5
2 * (1, 25х + 5у) = 20
Вычислить значение х в первом уравнении, подставить выражение во второе уравнение и вычислить у:
1,25 х = 5
х = 5/1,25
х = 4 (см) - первоначальная одна сторона прямоугольника.
2*(1,25 * 4 + 5у) = 20
10 + 10у = 20
10у = 10
у = 1 (см) - первоначальная вторая сторона прямоугольника.
Проверка:
2*(1,25*4 + 5*1)=2 * 10 = 20, верно.
2) Найти периметр прямоугольника:
Р = 2*(4 + 1) = 10 (см).
уравнение прямой, проходящей через две точки
(х-х₁)/(х-х₂)=(у-у₁)/(у-у₂)
а) (х-2)/(12-2)=(у-3)/(-2-3)
(х-2)/(10)=(у-3)/(-5); х-2=-2*(у-3);х-2=-2у+6; 2у=6+2-х; у=4-х/2
С(-14;11)
подставим ее координаты в уравнение прямой у=4-х/2
11=4+14/2; 11=11, верно. да. точка С(-14;11) принадлежит прямой у=4-х/2
б) D (165; –78)
подставим ее координаты в уравнение прямой у=4-х/2
-78=4+165/2; нет. точка D (165; –78) не принадлежит прямой у=4-х/2, т.к. справа дробное число, а слева целое