"Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры вычислялась с двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным с тройного интеграла."
z0 = integral(z*dx*dy*dz) / integral(dx*dy*dz)
причем по z пределы интегрирования от 0 до 2/3, поскольку поверхность sqrt(x^2+y^2)=2 пересекает конус 3z=sqrt(x^2+y^2) как раз при z=2/3
integral(z*dx*dy*dz) = integral(z*(pi*2^2-pi*9*z^2)*dz) = pi* integral((4z-9*z^3)*dz) = pi*(4z^2/2-9z^4/4) от 0 до 2/3 = pi*(4(2/3)^2/2-9*(2/3)^4/4) = 1.3962634
integral(dx*dy*dz) = integral((pi*2^2-pi*9*z^2)*dz) = pi* integral((4-9*z^2)*dz) = pi*(4z-9z^3/3) от 0 до 2/3 = pi*(4*(2/3)-9*(2/3)^3/3) = 5.5850536
z0 = 1.3962634/5.5850536 = 0.25
А) Найдите дробь со знаменателем 18 равную ей дроби 2/3.
18:3=6 - значит числитель и знаменатель надо домножить на 6
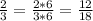
Б) Найдите дробь с числителем 7 равную ей дроби 1/9. Значит необходимо домножить числитель и знаменатель на 7.
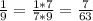
В) Можно ли найти дробь числитель которой натуральное число а знаменатель 121 равную ей дроби 5/11?
121:11=11 - кратно 11, значит надо домножить числитель и знаменатель на 11
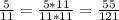
Г) Можно ли найти дробь знаменатель которой натуральное число а числитель 144 равную ей дроби 35/48 ?
144:48=3 - 144 кратно 48.
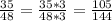
Нехай менше число дорівнює х, тоді друге число — 6х Складаємо рівняння
6х - х = 38;
5х = 38;
х = 38 : 5;
x = 7,6
Отже, менше число дорівнює , а 7,6 більше — 6 • 7,6 = 96.
Відповідь. Шукані числа — 7,6 і 96.
Но это не точно что правильно