Смешанные дроби
Числа, в состав которых входит целое число и правильная дробь, называются смешанными числами.Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа.Неправильную дробь можно записать в виде смешанного числа, для этого нужно числитель поделить на знаменатель. Полученное неполное частное будет целой частью смешанной дроби, остаток - числителем дробной части, а знаменатель исходной неправильной дроби - знаменателем дробной части.
Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
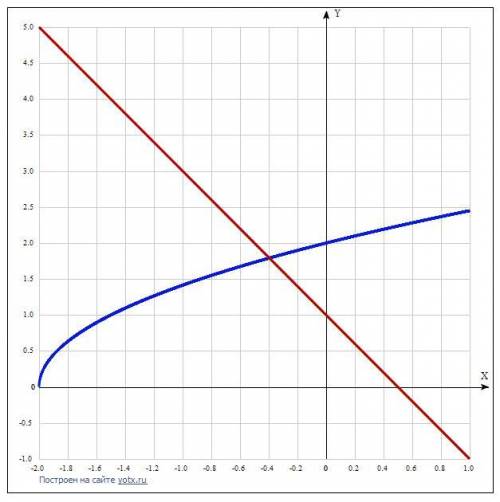
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
-6x-7=5+4x
-6x-4x=5+7
-10x=12
x=-5/6=-1,2
1/2x-2=5/6x-8
3x-12=5x-48
3x-5x=-48+12
-2x=-36
X=18