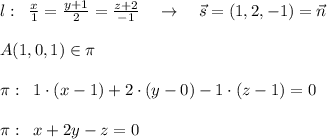
, лежит на перпендикуляре, проведённым из точки А к этой прямой. можно провести в плоскости, перпендикулярной прямой . будет нормальным вектором плоскости и точка А лежит в этой плоскости.
и плоскости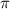 
. 
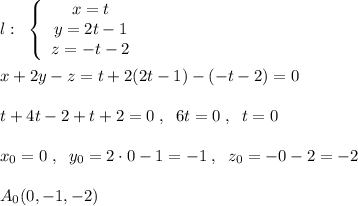
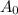является серединой отрезка 
.
.
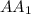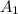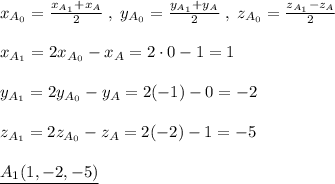
Если трапеция описана около окружности , то AD+BC=AB+CD
a+b = h+x , где х = CD ⇒ a+b = 4 и h + x = 4 .т.к. p = 8
a+b = 4 ⇒ a = 4 - 1 = 3 , a = 3
h + x = 4 ⇒ x = 4 - h
DE =AD-AE=a - b = 3 - 1 = 2
Δ CDE : CD² =CE² + DE²
x² = h² + 2²
( 4 - h )² = h² + 4
16 - 8·h + h² = h² + 4
16 - 8 h = 4
8 h = 16 - 4
8 h = 12
h = 12/ 8 = 3 / 2
r = h / 2 = (3 / 2 ) / 2 = 3/4