а) 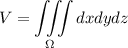 . В нашем случае
. В нашем случае 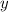 меняется от
меняется от 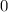 до
до 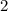 ,
,  меняется от
меняется от 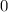 до
до 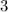 , а
, а  заключен между
заключен между 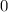 и
и 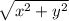 . По сути
. По сути  можно представлять себе как множество отрезков высоты
можно представлять себе как множество отрезков высоты 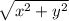 выпущенных из точки
выпущенных из точки 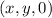 , причем эти точки берутся из прямоугольника
, причем эти точки берутся из прямоугольника ![[0,2]\times [0,3]](/tpl/images/4758/9834/e2d7a.png) .
.
Итак, 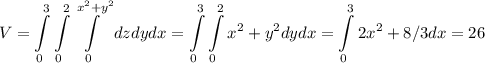 .
.
б) Здесь рассуждения такие же, только  представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости
представляет собой не прямоугольник, а область, ограниченную двумя <<перпендикулярными>> параболами на плоскости 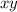 . Величина
. Величина  будет меняться от
будет меняться от 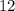 до минимального значения на
до минимального значения на  , что соответствует максимуму
, что соответствует максимуму 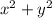 на
на  -- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке
-- то есть макисмальному удалению от начала координат. Это происходит в точке пересечения парабол -- точке 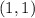 (а начало координат не подходит). Значит,
(а начало координат не подходит). Значит, 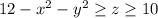 . Итого:
. Итого: 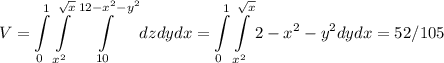 .
.
в) Здесь удобно сделать замену координат: 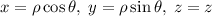 , тогда поверхности:
, тогда поверхности: 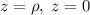 . Якобиан
. Якобиан 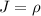 , имеем:
, имеем: 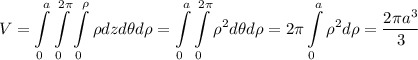 .
.
Я уже это писала
r - радиус окружности. α - угол , в градусах. π= 3.14. Длина дуги (L):
Формулы для окружности и круга
L = п*R*а / 180
ПОДСТАВЛЯЕМ
37,68 = (3,14*R* (180/4)) 180
37.68= (3.14*R*45) 180
выводим неизвестное
141.3R/180=37.68
141.3R=37.68*180
141.3R=6782.4
R=6782.4/141.3
R=48СМ
ОТВЕТ диаметр окружности 48см
Т.К. ГРАНИЦЫ ШАРА СОПРИКАСАЮТСЯ С КУБОМ, ПРОВЕДЯ ДИАМЕТР( 2* РАДИУС)Т.Е 20СМ, МОЖНО УВИДЕТЬ, ЧТО КАК И КУБ СТОРОНЫ БУДУТ ОДИНАКОВЫ, Т.Е ОБЪЕМ КУБА = ОБЪЕМУ ШАРА
V- КУБА (2*r) В ТРЕТЬЕЙ СТЕПЕНИ
2*10*2*10*2*10=8000см
во второй задаче немного неуверена
нет 9×2=18.
18+9= 27 Якось так