Пусть 
грн стоит один килограмм апельсинов, а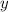 
грн — один килограмм лимонов. Тогда 5 кг апельсинов будут стоить 
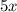грн, а 4 кг лимонов — 
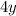грн, что вместе составляет 22 грн, то есть 
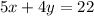. Также 6 кг апельсинов будут стоить 
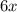грн, а 2 кг лимонов — 
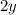грн, что вместе составляет 18 грн, то есть 
.
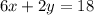Имеем систему из двух линейных уравнений:
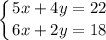
Домножим второе уравнение на 2:
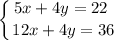
Вычтем из второго уравнения первое:
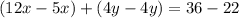
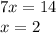
Тогда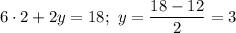 
Таким образом, 2 грн стоит один килограмм апельсинов и 3 грн стоит один килограмм лимонов.
ответ: 2 грн и 3 грн.
Пошаговое объяснение:
Пусть х (грн) - стоит 1 кг апельсинов, а у (грн) - стоит 1 кг лимонов, тогда 5 кг апельсинов стоят 5 х (грн) , а 6 кг лимонов стоят 6 у (грн) , вместе они стоят 150 грн, получаем уравнение 5 х+6 у=150. 4 кг апельсинов стоят 4 х (грн) , а 3 кг лимонов 3 у (грн) , раз 4 кг апельсинов дороже на 3 грн, то получим уравнение 4 х-3 у=3. Составим и решим систему уравнений:5 х+6 у=150,4 х-3 у=3;Решим систему сложения, умножив второе уравнение на 2, получим:5 х+6 у=150,8 х-6 у=6; 13 х=156,4 х-3 у=3; х=12,48-3 у=3; х=12,-3 у=-45; х=12, у=15.12 (грн) - стоит 1 кг апельсинов 15 (грн) - стоит 1 кг лимонов
,какаааек