1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Нет деления на ноль.
2. Пересечение с осью Х. Y=0 при х = 0 и х = -3. (ставим две точки на оси ОХ)
3. Пересечение с осью У. У(0) = 0. (ставим точку на оси ОУ)
4. Поведение на бесконечности.
limY(-∞) = - ∞ limY(+∞) = +∞ (слева вниз - справа вверх)
5. Исследование на чётность.
Y(-x) = -x³ +3x² ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² + 6*x = 3*x*(x-2).
Корень при Х1=0 и Х2= 2
Схема знаков производной.
_ (-∞)__(>0)__(х1=0)___(<0)___(x2=2)__(<0)_____(+∞)__
Функция убывает МЕЖДУ корнями.
7. Локальные экстремумы.
Максимум Ymax(-2)= 4 , минимум – Ymin(0)=0.
8. Интервалы возрастания и убывания.
Возрастает - Х∈(-∞;-2)∪(0;+∞) , убывает = Х∈(-2;0).
8. Вторая производная - Y"(x) = 6*х+6 =6*(x+1)=0.
Корень производной - точка перегиба Y"(x)= 0. Х= -1
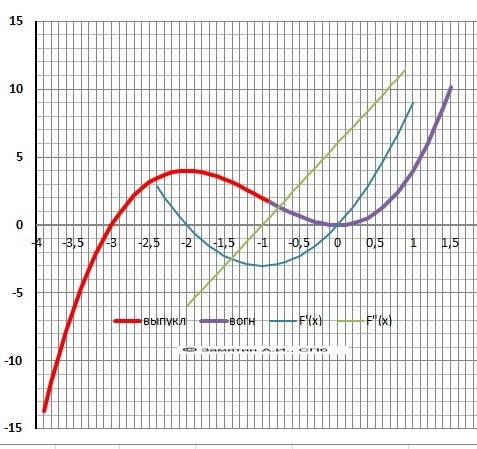
9. Выпуклая “горка» Х∈(-∞;-1), Вогнутая – «ложка» Х∈(-1;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. График в приложении.
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: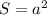
, где 
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: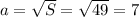 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
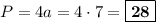см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть
см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,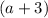 
см. Составляем уравнение:
Тогда другая сторона его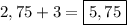
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда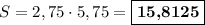
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
Тогда площадь прямоугольника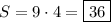
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: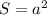
, где 
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 
см. Периметр квадрата равен длине его стороны, умноженной на 4: 
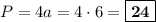см.