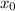. Так как функция монотонна на R, то для 
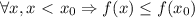. Пусть y - точная верхняя грань 
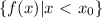. Для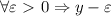 
не является верхней гранью данного множества. Поэтому 
.
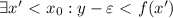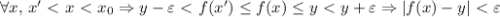
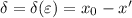, то получится как раз определение предела слева по Коши.
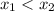- две точки разрыва, то 
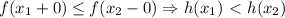. Отсюда разным точкам разрыва соответствуют различные h(x). Рациональных чисел счетное число, поэтому h(x) - не более чем счетно.
