Сложное событие B = {событие А появится в 8 независимых испытаниях хотя бы 2 раза, то есть не менее двух раз}.
Сложное событие C = {событие А появится в 8 независимых испытаниях менее двух раз}.
Событие C состоит из двух несовместных событий:
Событие C0 = {событие А появится в 8 независимых испытаниях ровно 0 раз, то есть не появится ни разу}.
Событие C1 = {событие А появится в 8 независимых испытаниях ровно 1 раз}.
В каждом из 8 испытаний вероятность того, что он появится событие A , равна p=0,1.
Следовательно, также в каждом из 8 испытаний вероятность того, что событие A не появится, равна
q=1−p=1−0,1=0,9.
Вероятность события C0 по формуле Бернулли равна
P(C0)=P8(0)=C08p0q8=8!0!8!⋅(0,1)0⋅(0,9)8=0,430467.
Вероятность события C1 по формуле Бернулли равна
P(C1)=P8(1)=C18p4q1=8!1!7!⋅(0,1)1⋅(0,9)7=0,382638.
События B и C противоположны. Следовательно, искомая вероятность равна
P(B)=1−P(C)=1−[P(C0)+P(C1)]==1−0,430467−0,382638≈0,19.
ответ. P=1—[P8(0)+P8(1)]=0,19.
Пошаговое объяснение:
Сложное событие B = {событие А появится в 8 независимых испытаниях хотя бы 2 раза, то есть не менее двух раз}.
Сложное событие C = {событие А появится в 8 независимых испытаниях менее двух раз}.
Событие C состоит из двух несовместных событий:
Событие C0 = {событие А появится в 8 независимых испытаниях ровно 0 раз, то есть не появится ни разу}.
Событие C1 = {событие А появится в 8 независимых испытаниях ровно 1 раз}.
В каждом из 8 испытаний вероятность того, что он появится событие A , равна p=0,1.
Следовательно, также в каждом из 8 испытаний вероятность того, что событие A не появится, равна
q=1−p=1−0,1=0,9.
Вероятность события C0 по формуле Бернулли равна
P(C0)=P8(0)=C08p0q8=8!0!8!⋅(0,1)0⋅(0,9)8=0,430467.
Вероятность события C1 по формуле Бернулли равна
P(C1)=P8(1)=C18p4q1=8!1!7!⋅(0,1)1⋅(0,9)7=0,382638.
События B и C противоположны. Следовательно, искомая вероятность равна
P(B)=1−P(C)=1−[P(C0)+P(C1)]==1−0,430467−0,382638≈0,19.
ответ. P=1—[P8(0)+P8(1)]=0,19.
1) Если внимательно посмотреть на закрашенную фигуру, то увидим, что ее периметр НЕ ОТЛИЧАЕТСЯ от периметра исходного прямоугольника, часть сторон которого продолжена пунктиром.
Он имеет параметры:
длина a : 7+3 = 10 (м); ширина b: 4+2=6 (м).
(Стороны отрезанного угла нашей фигуры равны противоположным сторонам прямоугольника, вырезанного в исходном прямоугольнике, которые мы должны были бы учесть при подсчете периметра!).
Р = 2(a+b) = 2·(10+6) = 32 (м)
Для проверки подсчитаем периметр ЗАКРАШЕННОЙ фигуры по отрезкам сторон:
Р = 7+2+3+4+10+6 = 10+6+10+6 = 2·(10+6) = 2·16 =32(м)
2). Площадь закрашенной фигуры равна разности площадей большого и вырезанного прямоугольников:
S = a·b -a₁·b₁ = 10·6 - 3·2 = 60 - 6 = 54 (кв.м)
Можно подсчитать площадь закрашенной фигуры как сумму площадей двух прямоугольников, на которые мы можем ее мысленно разделить. Большого со сторонами 7 и 6 м, и маленького со сторонами 4 и 3 м
S = S₁ + S₂ = 7·6 + 4·3 = 42 + 12 = 54 (кв.см)
ответ: периметр закрашенной фигуры 32см, площадь 54 кв.см
Пошаговое объяснение:
6^6:((3^2)^3*2^8)=6^6:(3^6*2^8)=6^6:(2^2*6^6)=6^6:(4*6^6)=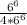 =
=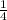 =0.25
=0.25
6^6:((3^2)^3*2^8)=6^6:(3^6*2^8) Упростим выражение путем умножения показателей степеней .
6^6:(3^6*2^8)=6^6:(2^2*6^6) Используем правила для показателей степеней чтобы упростить выражение
6^6:(2^2*6^6)=6^6:(4*6^6) Вычесляем степень
6^6:(4*6^6)=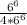 Запысиваем деление в виде дроби
Запысиваем деление в виде дроби