Пошаговое объяснение:
А)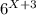 
>36 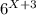> 6² основание 6 >1 , функция возрастающая, значит х+3>2 x>2-3 x> -1 Отв: х∈(-1;+∞) б) (1/5)ˣ⁺⁴<1/125 (1/5)ˣ⁺⁴<(1/5)³ основание 0< 1/5<1, функция убывающая, значит х+4>3 x>3-4 x>-1 Отв: х∈(-1;+∞) в)(5)ˣ²⁺ˣ > 1 (5)ˣ²⁺ˣ > 5⁰ основание 5>1, значит функция возрастающая, х²+х>0 x(x+1)>0 x∈(-∞;-1)∪(0;+∞) г)2ˣ²⁻ˣ⁺⁸>0 неравенство верно при любом х, т.к. показательная функция всегда положительна Отв: (-∞;+∞) д) (0,3)ˣ⁺⁵<-4 ,показательная функция всегда положительна, поэтому неравенство не имеет решения Отв: ∅ е) 2ˣ ·5ˣ ≤0, 001·(10ˣ⁻²)³ 2ˣ ·5ˣ ≤ 10⁻² · (10ˣ⁻²)³ 10ˣ ≤ 10⁻² · (10)³ˣ⁻⁶ 10ˣ ≤10³ˣ⁻⁸, основание 10>1, значит х<3x-8 -2x<-8 x>4 Отв (4:+∞) ж) 2ˣ⁺²-2ˣ⁺³ -2ˣ⁺⁴ >5ˣ⁺¹ -5ˣ⁺² 2ˣ⁺²(1-2-4) > 5ˣ⁺¹(1-5) 2ˣ⁺² ·(-5 )> 5ˣ⁺¹· (-4) 2ˣ⁺² : 4 > 5ˣ⁺¹:5 2ˣ⁺> 5ˣ, разделим обе части неравенства на 5ˣ>0, тогда (2/5)ˣ > 1, (2/5)ˣ >(2/5)⁰, основание 0<(2/5)<1. Значит функция убывающая, поэтому х< 0 Отв: (-∞;0)
Пошаговое объяснение:
Задание В1
1)АВСД-прямоугольник, значитАД=ВС=х , К-середина КС=х/2=0,5х
2)ΔКЕС подобен ΔДЕА по двум углам : ∠КЕС=∠ДЕА как вертикальные и ∠СКЕ=∠ЕДА как накрест лежащие при КД-секущей. В подобных треугольниках сходственные стороны пропорциональны :
КС/АД=СЕ/ЕА , 0,5х/х=ОС/10 , 0,5/1=ОС/10 ,ОС=5
3)АС=10+5=15
ΔАСД-прямоугольный , по т. Пифагора. х²+9²=15² , х²=225-81 , х²=144, х=12
Задание В2
S(АМNС)=0,5*h*(MN+AC) , где h-высота трапеции.
Т.к MN-средняя линия , то высота ΔАВС будет 2h , MN=1/2АС
60=0,5*h*(1/2АС+AC)
60=1/2*h*(3/2)*АС,
60=3/4 *h*АС
(60*4):3=h*АС
120=h*АС , умножим обе части на 1/2
120/1*2=1/2*h*АС
60=S(АВС)