Задание 1
Пусть х - работает первый насос, у - работает второй насос (производительность в минуту) , а Р - вся работа.
Р/(х+у)=20мин
Р/х=30
Из Р/х=30 найдем Х
х=Р/30
Подставим в первое уравнение:
Р/(Р/30+у)=20
Р=20*(Р/30+у)
Р=2/3Р+20у
20у=Р/3
у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть
ответ. 60 минут
Задание 2
( 7,85х - 12,4х ) * (-1 9/91) = - 2 11/12 - 1 2/3
-4.55х* (- 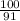 ) =
) = 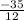 -
- 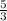
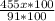 =
= 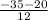
5x= 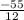
x= 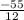 *
* 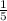
x= 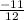
269.36см²
Пошаговое объяснение:
В задаче не указано в чем дан периметр (см, м, мм), поэтому буду исходить из того, что это 66.6 см
У прямоугольника стороны попарно равны, его периметр равен сумме всех его сторон, поэтому: Р=2*(а+в), где а и в - ширина и длина прямоугольника
Пусть ширина прямоугольника - х,
тогда длина прямоугольника - 1,25х
2*(х+1,25х)=66,6
2х+2,5х=66,6
4,5х=66,6
х=66,6:4,5
х=14,8 (см) - ширина прямоугольника
1,25х=1,25*14,8=18,5 (см) - длина прямоугольника
S (площадь) прямоугольника = а*в
S=14.8*18.5=269.36см²
x=0
Пошаговое объяснение:
Разделим обе части уравнения на 27^x
8^x/27^x + 18^x/27^x=2
(8/27)^x + (18/27)^x=2
(2/3)^(3x) +(2/3)^x=2
Замена (2/3)^x=t
t^3+t=2
t^3+t-2=0
Очевидно, что один корень этого уравнения равен 1. Разделим t^3+t-2 на t-1
получим t^2+t+2. Таким образом (t-1)(t^2+t+2)=0 Уравнение t^2+t+2=0 действительных корней не имеет, т. к. дискриминант меньше 0.
(2/3)^x=1
x=0
ответ: х=0