2. Постройте системы двух линейных уравнений, в которых пара числе будет являться решением:

а) (-2; 3)

б) (6; 1)

в) (4; -3)

👇

Открыть все ответы

Ответ:

NeZoXshock

10.12.2021

ответ: $\dfrac{63}{40}$ Пошаговое объяснение:Нарисуем сначала нашу область D.1) y = x

Это прямая, которая проходит через начало координат и находится под углом в 45 градусов от полуоси Ох, проходит например через точку (1 1)

2) y = x² - 2

Это парабола (перед нами квадратный трехчлен) Вершина в точке (0 2), образована путем смещения всех точек параболы у = х² на 2 единицы вниз

Смотрите вложение!

Мы интегрируем по красной области1) Запишем границы

х меняется от -1 до 2 это границы, х координаты точек пересечения (видно из графика)

Для того, чтобы из найти решим уравнение

$\displaystyle x^2-2=x\\x^2-x-2=0\\x^2-2x+x-2=0\\x(x-2)+(x-2)=0\\(x+1)(x-2)=0\\\left [ {{x=-1} \atop {x=2}} \right.$

Это будут первые границы по х

Границы по у - это функции от х. Снизу (нижняя граница) функция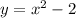 y=x^2-2 а верхняя граница функция

Тогда запишем двойной интеграл как пару интегралов, зная границы

$\displaystyle \iint\limits_D xy^2dxdy=\int\limits^2_{-1}dx\int\limits^x_{x^2-2x}xy^2dy$

Решим данный интеграл

1 Проинтегрируем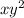 xy^2 по у

$\displaystyle\int xy^2dy=x\displaystyle\inty^2dy=x\cdot\dfrac13y^3=\dfrac13xy^3$

константу не пишу специально, так как сейчас буду писать пределы

2 Вычислим

$\dfrac13xy^3\Bigg|^x_{x^2-2}=\dfrac13x\cdotx^3-\dfrac13x\cdot(x^2-2)^3=\dfrac13x\Big(x^3-(x^2-2)^2\Big)=-\dfrac13x^7+2x^5+\dfrac13x^4-4x^3+\dfrac83x$

3 Проинтегрируем полученную функцию по х

$\displaystyle \int\Bigg(-\dfrac13x^7+2x^5+\dfrac13x^4-4x^3+\dfrac83x\Bigg)dx=\\=-\int\dfrac13x^7dx+\int2x^5dx+\int\dfrac13x^4dx-\int4x^3dx+\int\dfrac83xdx=\\=-\dfrac13\int x^7dx+2\int x^5dx+\dfrac13\int x^4dx-4\int x^3dx+\dfrac83\int xdx=\\=-\dfrac1{24}x^8+\dfrac13x^6+\dfrac1{15}x^5-x^4+\dfrac43x^2$

4 Подставляем пределы и считаем

$-\dfrac1{24}x^8+\dfrac13x^6+\dfrac1{15}x^5-x^4+\dfrac43x^2\Bigg|^2_{-1}=-\dfrac{32}3+\dfrac{64}3+\dfrac{32}{15}-16+\dfrac{16}{3}=\dfrac{63}{40}$

Вычислить двойной интеграл xy^2 D: y=x, x^2 - 2 =y

4,4(83 оценок)

Ответ:

An55551

10.12.2021

уравнение:

Пусть скорость автобуса x км/ч, тогда скорость грузовой машины (x+17) км/ч. Скорость сближения x+x+17 = 2x+17 км/ч. Встретились через 3 часа, то есть

(2x+17)\cdot3=453\\2x+17=151\\2x=134\\x=67

Скорость автобуса 67 км/ч, грузовой машины 67+17 = 84 км/ч система уравнений:

Пусть скорость автобуса x км/ч, скорость грузовой машины y км/ч.

Скорость грузовой машины на 17 км/ч больше скорости автобуса, т.е. y-x = 17.

Встретились через 3 часа, то есть (x+y)*3 = 453.

Составим и решим систему уравнений

\begin{cases}y-x=17\\(x+y)\cdot3=453\end{cases}\Rightarrow\begin{cases}x=y-17\\(y-17+y)\cdot3=453\end{cases}(y-17+y)\cdot3=453\\2y-17=151\\2y=168\\y=84\\\begin{cases}x=84-17=67\\y=84\end{cases}

Скорость автобуса 67 км/ч, грузовой машины 84 км/ч.

Пошаговое объяснение:

4,4(27 оценок)

Это интересно:

Здоровье

24.10.2021

Как выжить при смещенных дисках...

Хобби-и-рукоделие

22.07.2021

Как сделать флаг: простой шаг за шагом гид...

Дом-и-сад

16.01.2020