Частное решение дифференциального уравнения:
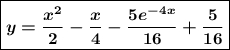
Примечание:
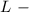 преобразование Лапласа
преобразование Лапласа
Функция 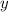 зависит от
зависит от  .
.
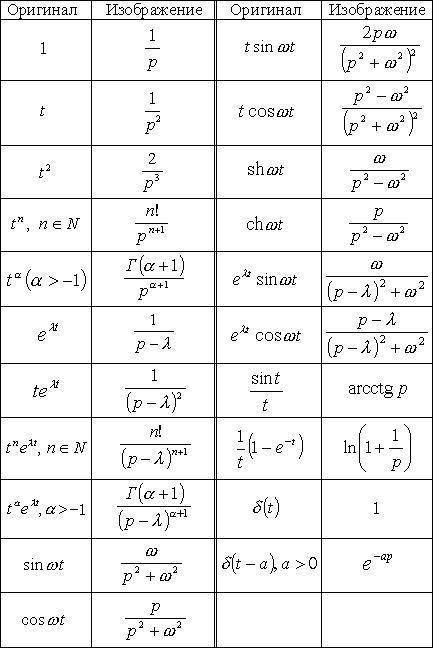
Прямое преобразование Лапласа (связь между оригиналами и изображениями):

По свойствам преобразования Лапласа:
Если  , то
, то 
Пошаговое объяснение:
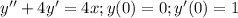
Для нахождения частного решения данного дифференциального уравнения воспользуемся методом операционного исчисления, а именно преобразованием Лапласа:

Дифференцирования оригинала:
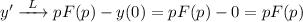
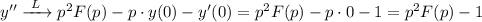
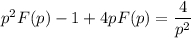
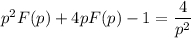
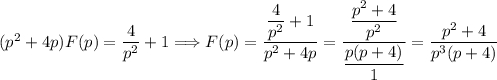
Раскладываем дробь на простейшие:
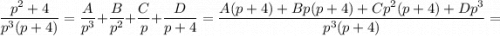

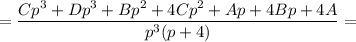
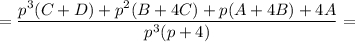
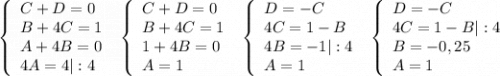
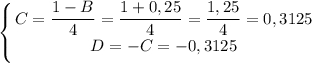


Таким образом 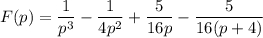
Выполним обратное преобразование Лапласа:
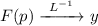
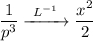
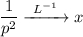
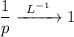
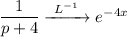
Тогда исходная функция равна:
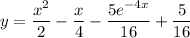
Т.к. в двух рядах 140 кустов, то во втором ряду после пересадки будет (140-0,875х) кустов. Составляем уравнение:
0,875х=140-0,875х (т.к. по условию в обоих рядах кустов поровну)
0,875х+0,875х=140
1,75х=140
х=140:1,75
х=80
⇒в первом ряду 80 кустов, тогда во втором - 60 кустов;
12,5% от 80 это 80*0,125=10, т.е. 10 кустов пересадили и стало по 70 кустов в каждом ряду.
ответ: в первом ряду было 80 кустов смородины