Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 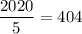 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 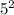 :
:
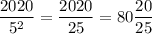
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 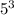 :
:
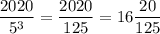
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 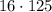 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 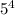 :
:
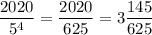
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 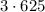 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 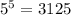 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
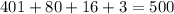
Значит, число 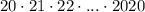 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 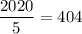 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 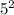 :
:
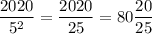
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 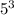 :
:
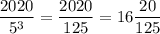
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 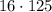 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 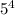 :
:
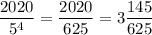
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 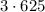 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 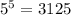 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
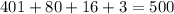
Значит, число 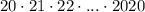 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
Задание 1.
1) 6*18=108 - сумма первых шести чисел
2) 7*22=154 - сумма всех семи чисел
3) 154-108=46 - седьмое число
ответ: 46
Задание 2.
Среднее геометрическое чисел а и b равно √(ab)
a=200, b=512
Находим среднее геометрическое 200 и 512:
ответ: 320
Задание 3.
1) 4м=400 см
2) 15м=1 500 см
3) 400*1 500=600 000 (см²) - площадь прямоугольной площадки
4) 5*10=50 (см²) - площадь одной плитки
5) 600 000:50=12 000 (шт.) - плиток потребуется
ответ: 12 000 шт.
Задание 4.
1) 13+21=34 (чел.) - абоненты МТС и МЕГАФОН
2) 34-29=5 (чел.) - одновременно являются абонентами МТС и МЕГАФОН
Утверждения:
1 - верно (ровно 5 сотрудников - абоненты и МТС и МЕГАФОН -см. 2 действие);
2 - неверно (нет среди сотрудников ни одного, кто не был бы абонентом МТС или МЕГАФОН;
3- неверно (только 5 человек - см. 2 действие);
4 - неверно (см. 2 действие)
ответ: 234
Подробнее - на -
Пошаговое объяснение: