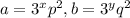, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
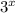, получим уравнение 
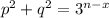. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 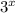, имеем 
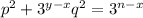. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
2017, 2018, ... 2030, (2031, ... , 20179999)
(2031, ... , 20179999), 20180000, ... , 2018013
В скобки взяты одинаковые части двух последовательностей. При вычитании произведений цифр каждого числа первой последовательности из произведений цифр этого же числа второй последовательности, мы получим нуль.
Осталось перемножить все цифры оставшихся чисел первой и второй последовательности и найти разность.
Произведение цифр каждого числа первой последовательности 2017, 2018, ..., 2029, 2030 равно нулю. Также равно нулю произведение цифр всех оставшихся чисел второй последовательности - 20180000, 20180001, ... , 20180013. Произведения цифр чисел равны нулю, т.к. в каждое число входит цифра 0.
Следовательно, сумма всех чисел, выписанных в тетрадь Фоксом, равно нулю.