ответ: город A от города B находися на расстоянии 44 км 444 м
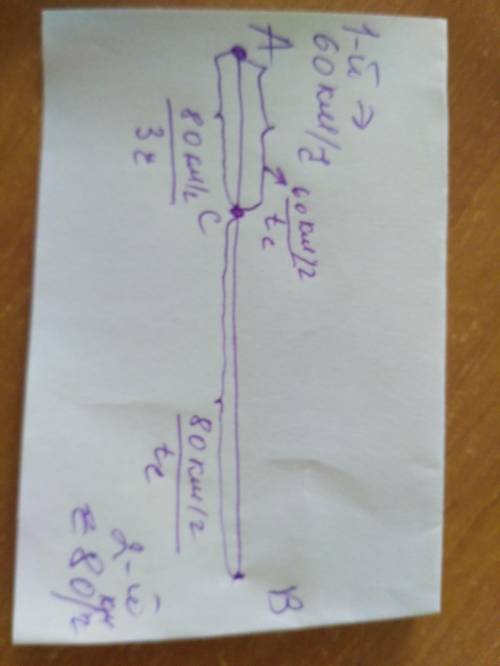
Решение: Пусть первый автомобиль имел скорость 60 км/ч и выехал из города А, соответственно второй выехал из города В со скоростью 80км/ч.
Расстояние, которое проехал первый из А до С равно расстоянию, что проехал второй из города С до А. Пусть t(C)- время первого авто до города С, тогда S(AC)=60:t(c) и, по условию задачи, S(CB)=80:3
S(AC)= S(CB);
80:3=60:t(C);
t(C)=60*3:80=9/2(ч)
Найдем расстояние от В до А, которое проделал второй автомобиль:
S(AB)= S(AC) +(CB);
S(AB)=80:9/2+80/3=80*2/9 + 80*3/9=(160+240)/9=400/9≈44,444(км)
А 210 км В 232 км С
> 63 км/ч х км/ч <
40 мин = 40/60 ч = 2/3 ч - время остановки
Пусть х км/ч - скорость мотоциклиста, тогда 232/х ч - время на путь от города С до города В, 210/63 ч - время на путь от города А до города В. Уравнение:
210/63 - 232/х = 2/3
210 · х - 232 · 63 = 2/3 · 63 · х
210х - 14616 = 42х
210х - 42х = 14616
168х = 14616
х = 14616 : 168
х = 87
ответ: 87 км/ч - скорость мотоциклиста.
Проверка:
210/63 - 232/87 = 2/3
6090/1827 - 4872/1827 = 2/3
1218/1827 = 2/3 - сократили на 609