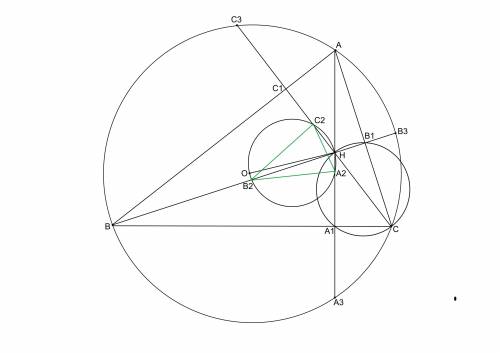
1) Все середины хорд, проходящих через точку внутри окружности (пусть это точка H, пока не важно, что это ортоцентр ΔABC) лежат на окружности, построенной на отрезке OH, как на диаметре. См. чертеж, О - центр большой окружности.
Например, хорда СС3, середина С2, угол OC2H прямой, так как диаметр, который делит хорду пополам, перпендикулярен ей. Поэтому С2 лежит на указанной окружности. Это справедливо для любой хорды, проходящей через точку H
2) Таким образом, если соединить середины хорд AA3, BB3 и CC3, то получится ΔA2B2C2, вписанный в окружность, построенную на отрезке ОН, как на диаметре. Разумеется, на этой окружности лежат и точки O и H.
3) Поскольку в этой задаче точка H - ортоцентр ΔABC, очень легко установить соответствие между углами ΔABC и ΔA2B2C2.
Проще всего увидеть, что ∠A2B2C2 =∠ABC, так как оба составляют 180° в сумме с ∠C1HA1.
В самом деле, четырехугольник B2C2HA2 вписанный, поэтому ∠A2B2C2 + ∠C1HA1 = 180°,
В четырехугольнике BC1HA1 два угла прямые, поэтому сумма двух других углов тоже 180°
∠ABC + ∠C1HA1=180°,
Поэтому ∠ABC = ∠A2B2C2;
4) ∠B2C2A2 = ∠B2HA2 оба угла вписаные и опираются на одну и ту же дугу. Поэтому ∠B2C2A2 = 180° - ∠B1HA1 = ∠BCA; последнее равенство справедливо по такой же причине, что и в пункте 3) - в четырехугольнике BC1HA1 два угла прямые, поэтому сумма двух других углов тоже 180°.
Поскольку два угла ΔABC и ΔA2B2C2 равные, эти треугольники подобны, чтд
Пошаговое объяснение:
1. Образующая конуса (формула согласно теореме Пифагора):
L²=R²+H², где
R - радиус, см; H - высота, см.
10²=6²+H²; H=√(100-36)=√64=8 см
Объём конуса:
V=1/3 ·πR²·H=1/3 ·π·36·8=π·12·8=96π≈96·3,14≈301,44 см³
2. Площадь сечения:
S=H·2R, где
H - высота, см; R - радиус цилиндра, см.
R=2,5H
80=H·2·2,5H
H²=80/5
H²=16
H=±√16=4 см (-4 - не подходит по смыслу задачи).
Радиус:
R=2,5H=2,5·4=10 см
Объём цилиндра:
V=πR²·H=π·10²·4=400π≈400·3,14≈1256 см³
3. Объём шара:
V=(πD³)/6, где D - диаметр шара, см.
Для более лёгкого счёта переведём диаметр в радиус:
R=D/2=20/2=10 см
V=4/3 ·πR³, где R - радиус шара, см.
V=4/3 ·π·10³=(4000π)/3≈(4000·3,14)/3≈12560/3≈4 186,67 см³
S = 600 см2, P = 100 см.
Объяснение :
V = a * b * h, где а - длина, b - ширина, h - высота.
h = V / a * b
h = 7200 / 30 * 20 = 7200 / 600 = 12 см.
ответ: высота коробки 12 см.
2) Узнаем площадь дна коробки, если известны длина и ширина:
S = a * b, где а - длина, b - ширина.
S = 20 * 30 = 600 см2.
Теперь определим периметр дна коробки:
P = 2a + 2b, где а - длина, b - ширина.
P = 2 * 20 + 2 * 30 = 40 + 60 = 100 см.
ответ: S = 600 см2, P = 100 см.