Схема (смотри приложение) . На мой взгляд , это более эффективный чем метод побора.
Метод подбора . По условию ясно видно: 1) I голова съела больше всех конфет ( в 3 раза больше, чем III голова) 2) II голова - на 3 кг больше , чем III голова 3) III голова съела меньше всех конфет ( в 3 раза меньше , чем I голова)
Т.е. нужно подобрать три числа , сумма которых равна 48 . При этом наибольшее число делится на 3 , но ощутимо меньше 48 . От этого и будем отталкиваться: 1) Допустим I голова съела 30 кг конфет . 30 : 3 = 10 (кг) съела III голова 10 +3 = 13 (кг) съела II голова 30 + 13 + 10 = 53 (кг) > 48 кг ⇒ не удовлетворяет условию задачи ⇒ следующее число кг конфет для I головы должно быть < 30 2) Допустим I голова съела 27 кг конфет. 27 : 3 = 9 (кг) съела III голова 9 + 3 = 12 (кг) съела II голова 27 + 12 + 9 = 48 (кг) удовлетворяет условию задачи.
ответ: 27 кг конфет съела первая голова дракона, 12 кг конфет съела вторая голова и 9 кг - третья голова .
Первая бригада - 90 мешков,
Вторая бригада - 60 мешков.
Пошаговое объяснение:
Общее количество мешков: 150 шт.
Собрала картофеля первая бригада - 4500 кг
Собрала картофеля вторая бригада - 3000 кг
Сначала найдём, сколько килограмм картофеля вместилось в 150 мешков:
4500 + 3000 = 7500 кг
Теперь задачу можно решить пропорцией. Возьмём, к примеру, первую бригаду:
7500 кг = 150 шт.
4500 кг = х шт.
х =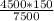 = 90 шт.
= 90 шт.
Количество мешков, собранных второй бригадой, можно посчитать также, но мы поступим иначе:
150 - 90 = 60 шт.
От общего количество отняли известное.
Задача решена!