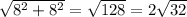, а сторона основания равна удвоенному катету, лежащему на этом основании, то есть 8*2=16, тогда площадь одной боковой грани равна 
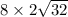, а площадь всех боковых граней равна сумме четырех этих площадей. В свою очередь полная площадь равна сумме площади боковых граней и площади основания, где площадь основания равна 16*16=4^4=2^8=256, поэтому площадь полной поверхности равна 
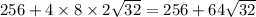Будем надеяться, что я не ошибся в вычислениях.
Кузнечик делает 7 прыжков, значит k = 7. Всевозможные точки, в которых может оказаться кузнечик, описываются формулой : 7+2n, -k≤n≤0.
Эти точки: -7, -5, -3, -1, 1, 3, 5, 7.
Всего из k+1 = 7+1 = 8.
ответ: 8.
Теперь рассмотрим, сколько существует точек, в которых кузнечик может оказаться, сделав 7 прыжков:
Пусть изначально кузнечик находится в точке 0.
Тогда после первого прыжка он может оказаться либо в точке 1, либо в точке -1. То есть всего 2 варианта: 1; -1.
2 прыжок: из точки 1 кузнечик может прыгнуть либо в 0, либо в 2. Из точки -1 - в точку -2 или 0. Поэтому всего 3 варианта: -2, 0, 2.
3 прыжок: из точки -2 кузнечик может попасть либо в -3, либо в -1; из точки 0 - либо в 1, либо в -1; из точки 2 - либо в 1, либо в 3. получаем 4 варианта: -3, -1, 1, 3.
4 прыжок: соответственно получаем 5 вариантов: -4, -2, 0, 2, 4.
5 прыжок: будет 6 вариантов: -5, -3, -1, 1, 3, 5.
6 прыжок: 8 вариантов: -6, -4, -5, -2, 0, 2, 4, 6.
7 прыжок: 10 вариантов: -7, -5, -3, -6, -4, -1, 1, 3, 5, 7