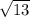Решение: Обозначим первое натуральное число за (х), тогда второе натуральное число равно: (х+1) Попробуем доказать, что произведение таких чисел равно 2017: Умножим первое число на второе и приравняем их к числу 2017 х*(х+1)=2017 х^2+x=2017 x^2+x-2017=0 x1,2=(-1+-D)/2*1 D=√(1-4*1*-2017)=√(1+8068)=√8069≈89,2 - не натуральное число, подставив дискриминант в выражение х1,2=(-1+-89,2)/2 получим первое число не натуральное, второе число также не получится натуральным числом. Отсюда можно сделать вывод, что произведение чисел, указанных в задании не может быть равным 2017
Решение: Обозначим первое натуральное число за (х), тогда второе натуральное число равно: (х+1) Попробуем доказать, что произведение таких чисел равно 2017: Умножим первое число на второе и приравняем их к числу 2017 х*(х+1)=2017 х^2+x=2017 x^2+x-2017=0 x1,2=(-1+-D)/2*1 D=√(1-4*1*-2017)=√(1+8068)=√8069≈89,2 - не натуральное число, подставив дискриминант в выражение х1,2=(-1+-89,2)/2 получим первое число не натуральное, второе число также не получится натуральным числом. Отсюда можно сделать вывод, что произведение чисел, указанных в задании не может быть равным 2017
Відповідь:
Покрокове пояснення:
1. 3a + b = {3*(-3) + 4; 3*10 + (-8)} = {-5; 22}
2. |AB| =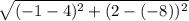 =
= 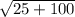 =
= 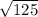 = 5
= 5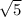
3. x = (2 + (-1))/2 = 0,5
y = (3 + 5)/2 = 4
M(0,5; 4)
|AB| =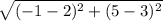 =
= 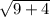 =
=