(x:2)*302=82478
(x:2)=82478:302
x= 273,10596026490 (с остатком)
(273,10596026490:2)*302=82478
82478=82478
И ВТОРОЙ ПРИМЕР Я ПРИДУ ИЩМЕНЮ ВОПРОС И ДОБАВЛЮ ИЛИ В КОМЕНТЕ НАПИШУ ПАТОМУ МНЕ КУШАТЬ НАДО
Пошаговое объяснение:
я чот так и не поняла что делать но я дуиаю здесь уравнение решить...
0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
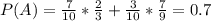
0.7
Пошаговое объяснение:
всего в коробке 7+3=10 шаров
вероятность вынуть первый белый шар равна 7/10
вероятность вынуть первый черный шар равна 3/10
А теперь смотрим, если первым вытянули белый шар, то в коробке осталось 6 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 6/9=2/3.
Если первым вытянули черный шар, то в коробке осталось 7 белых шаров из 9 оставшихся, тогда второй белый шар будет вынут с вероятностью 7/9
Задача на полную вероятность:
Гипотезы:
B - первым вынули белый шар.
C - первым вынули черный шар.
P(B)=7/10
P(C)=3/10
A-вторым вынули белый шар.
Условные вероятности:
A/B - вторым вынули белый шар, при условии что первым вынули белый шар.
A/C-вторым вынули белый шар, при условии что первым вынули черный шар.
P(A/B)=2/3
P(A/C)=7/9
Формула полной вероятности:
P(A)=P(B)*P(A/B)+P(C)*P(A/C)
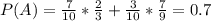
Пошаговое объяснение:
Я не очень хорошо понимаю это задание но попробовала его как-то решить.