190 прямых
Пошаговое объяснение:
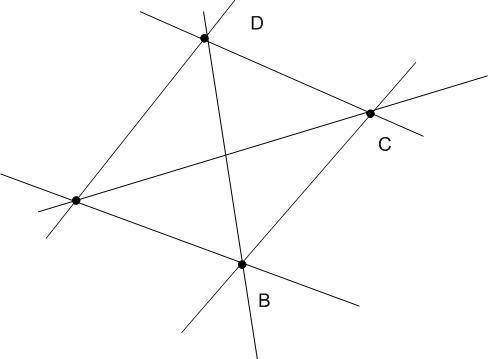
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
1)начертить отрезок МР
2)циркулем начертить окружность с центром в т.М радиусом, несколько бОльшим, чем предполагаемая середина отрезка
3)не изменяя расстояние циркуля,начертить окружность с центром в т.Р
4)окружности пересекутся в 2 точках.
5)через эти точки провести прямую-она разделит отрезок МР ровно пополам. Обозначим эту точку пересечения прямой и отрезка МР как точку А.
разделить отрезок АР пополам по той же схеме, повторив шаги 1)-5).
обозначим середину отрезка АР точкой В
разведем "ножки" циркуля на расстояние, равное отрезку МВ и "перенесем" это расстояние на числовой луч, выбрав за исходную точку начало луча-точку О.
вторая "ножка" циркуля отложит на луче расстояние, равное МВ. поставим на луче в этом месте точку К
расстояние ОК=МВ=3/4МР