n<arccos(R₁/R₂)/180
Пошаговое объяснение:
вероятность и геомтрия.
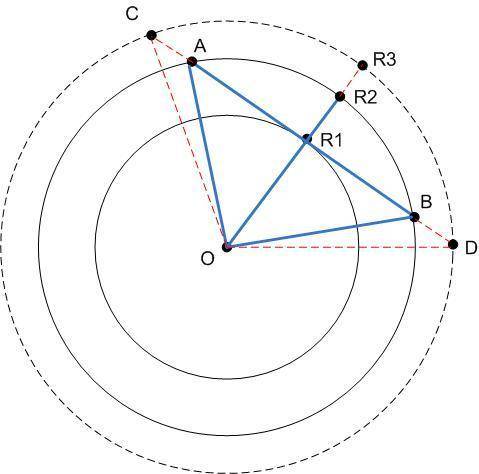
Посмотрим на рисунок. Назовем событие благоприятным, если точки А и В попадают (одновременно) в сегмент большой окружности AR₂B. Причем нарисованный вариант - имеет максимальную длину дуги (при данных величинах радиусов R₁ R₂), опирающуюся на хорду lABl, еще не пересекающую малую окружность ( lABl только касается меньшей окружности в т R₁).
Вопрос: в каких единицах будем измерять благоприятные (да и все возможные случаи)? В количестве точек - не реально. Точек, что на вышеуказанной дуге, что на всей окружности бесконечно много. Раз в количестве тчек не получается, то будем сравнивать длины дуг!
Итак вероятность n непересечения будет равне:
n=l₀₁/l₀₀, где
l₀₁ - длина дуги AR₁B (количество благоприятных случаев)
l₀₀ - длина большой окружности (количество всех возможных случаев)
С l₀₀ все просто:
l₀₀=2πR₂
Вычислим длину "благоприятной" дуги l₀₁ .
Дуга AR₂B опирается на центральный угол AOB. Найдем этот угол.
Рассмотрим Δ OAR₁. Этот треугольник прямоугольный (прямой угол ∠R₁, т.к. lABl -касательная к малой окружности в т.R₁).
Катет lOR₁l=R₁ (радиусу малой окружности), гипотенуза lOAl=R₂ - радису большой окружности.
lOR₁l/ lOAl=R₁/R₂=cos(∠AOR₁).
∠AOR₁=arccos(R₁/R₂) ⇒ ∠AOB=2*arccos(R₁/R₂).
Длина дуги AR₂B:
l₀₁=2*arccos(R₁/R₂)*2πR₂/360=arccos(R₁/R₂)*2πR₂/180 (запишем так для наглядности);
n=l₀₁/l₀₀, ⇒ n = (arccos(R₁/R₂)*(2πR₂)/(180) : 2πR₂) =arccos(R₁/R₂)/180;
n=arccos(R₁/R₂)/180. (1)
Замечание:
На рисунке есть еще одна окружность с радиусом R₃>R₂>R₁. Исходя из этого рисунка наблюдаем динамику роста "благоприятного" сектора при увеличении радиуса бОльшей окружности.
Проверка:
Подставим в полученную формулу отношение R₁/R₂=0,01 (R₂>>R1).
Посчитаем вероятность:
n=arccos(0,01)/180≈0,497.
Т.е. при росте "большой" окружности растет и длина "благоприятного" сектора, и в пределе этот сектор становится равным 1/2 длины окружности (вероятность становится равной 0.5 или 50%).
Справедливости ради формулу (1) надо записать вот так:
n<arccos(R₁/R₂)/180,
т.к. знак "=" - это предельный случай, точка касания, а не пересечения.
Пятеро каменщиков вначале рабочей недели получили равное количество кирпича. Когда трое из них израсходовали по 326 кирпичей, то у них осталось столько кирпичей, сколько вначале получили другие два каменщика. Сколько всего кирпичей получили каменщики вначале недели?
Решение
По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:
326 * 3 = 978(кирпичей);
далее вычисляем, сколько всего было кирпичей:
978 * 5 = 4890.
ответ: вначале недели каменщики получили всего 4890 кирпичей.
Пошаговое объяснение:
1) 75% = 3/4
2) 20% =1/5
3) 60% = 3/5
4) 92% = 23/25
5) 44% = 11/25
6) 87% = 87/100