Пошаговое объяснение:
1. производные
(5x³-3x⁹)' = 5*3x² -3*9x⁸ = 15x² -27x⁸
![\displaystyle (6\sqrt[3]{x} +4\sqrt{x} )' = (6x^{1/3} +4x^{1/2})'=6\frac{1}{3}x^{-2/3} +4\frac{1}{2\sqrt{x} } =\frac{2}{x^{2/3}} +\frac{2}{\sqrt{x} }](/tpl/images/1763/9786/45f1d.png)
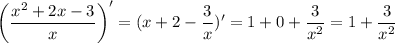
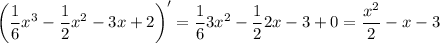
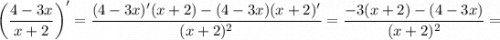

(e⁻⁵ˣ)' = -5e⁻⁵ˣ
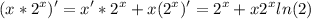
2.
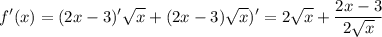
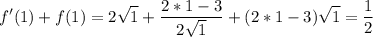
3. уравнение касательной
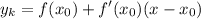
f'(x) = -2x+6
f(x₀) = f(-2) = -8
f'(x₀) = f'(-2) = 10
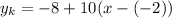
или
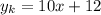
5.
для всего ниже потребуется производная
f'(x) = (x³-2x²+x+3)' = 3x² -4x +1
а) стационарные точки
3x² -4x +1 = 0 ⇒ x₁ = 1; x₂ = 1/3
б) экстремумы
f(1) = 3 - минимум
f(1/3) = 85/27 максимум
в) возрастание и убывание
по стационарным точкам получили три интервала
смотрим на каждом значение производной и определяем возрастание или убывание функции
(-∞ ;1/3) f'(0) =1 > 0 функция возрастает
(1/3; 1) f'(2/3) = -1/3 < 0 функция убывает
(1; +∞) f'(10) = 261 > 0 функция возрастает
г) график прилагается (таблицу уже сами построите)
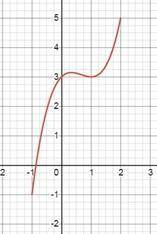
Ниже читай
Пошаговое объяснение:
Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору. Утверждение появляется как Предложение 47 в «Началах» Евклида.
Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третьей стороны, является прямоугольным.
Существует ряд обобщений данной теоремы — для произвольных треугольников, для фигур в пространствах высших размерностей. В неевклидовых геометриях теорема не выполняется