80 м/мин-70 м/мин=10 м/мин (разница скоростей) 30 м+70 м=100 м (разница расстояний) 100 м:10 м/мин=10 мин (за 10 минут возникнет разница расстояний 100 м при разнице скоростей в 10 м/мин), то есть через 10 минут после выхода из дома при скорости 80 м/мин Оскар будет в 70 м за мостом или при скорости 70 м/мин в 30 м перед мостом. 70 м/мин*10 мин=700 м (пройдет за 10 мин со скоростью 70 м/мин) 700 м+30 м=730 м (от дома до моста) ИЛИ 80 м/мин*10 мин=800 м 800 м-70 м=730 м ответ: от дома Оскара до моста 730 метров
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
Приведем к ступенчатому виду. Применяем операцию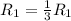 к
к  (к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию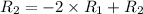 к
к  (ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию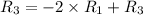 к
к  (к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию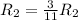 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию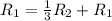 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Применяем операцию к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию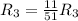 к
к  для того, чтобы сделать некоторые элементы строки равными 1.
для того, чтобы сделать некоторые элементы строки равными 1.
Применяем операцию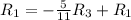 к
к  для того, чтобы сделать некоторые элементы строки равными 0.
для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию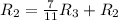 к
к  для того, чтобы сделать некоторые элементы равными 0.
для того, чтобы сделать некоторые элементы равными 0.
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
Решением является множество упорядоченных пар, которые удовлетворяют системе.